Пусть функция 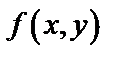 определена в ограниченной замкнутой области (S) плоскости (XOY).
определена в ограниченной замкнутой области (S) плоскости (XOY).
Интегральной суммой называется сумма вида 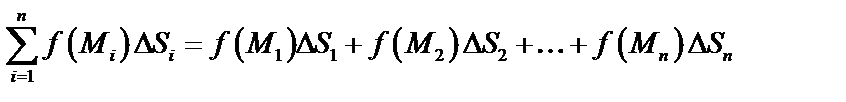 ,
,
тогда 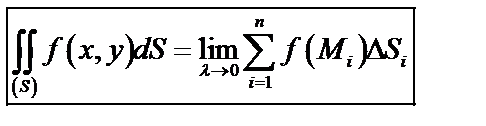 ,
,
где 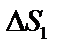 ,
, 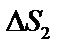 , …,
, …, 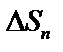 – площади частичных областей,
– площади частичных областей,
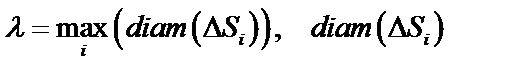 – диаметр
– диаметр 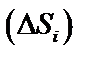 ,
,
точка 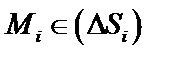 элементарной области.
элементарной области.
В декартовых координатах двойной интеграл записывают в виде 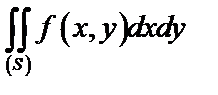 .
.
Различают два основных вида области интегрирования.
1) Область интегрирования (S) ограничена слева и справа прямыми 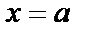 и
и 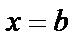
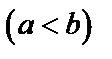 , а снизу и сверху – непрерывными кривыми
, а снизу и сверху – непрерывными кривыми 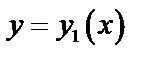 и
и 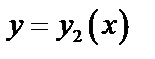
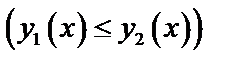 , каждая из которой пересекается прямой, параллельной оси
, каждая из которой пересекается прямой, параллельной оси 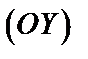 , только в одной точке (рис. 7).
, только в одной точке (рис. 7).
Для данной области двойной интеграл вычисляется по формуле:
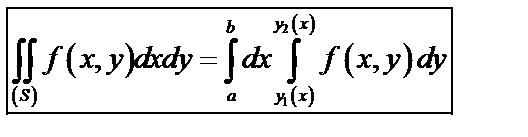 , (40)
, (40)
причем сначала вычисляется интеграл 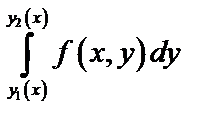 , где
, где 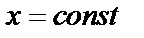 .
.
2) Область интегрирования (S) ограничена снизу и сверху прямыми 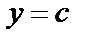 и
и 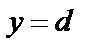
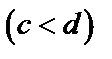 , а слева и справа – непрерывными кривыми
, а слева и справа – непрерывными кривыми 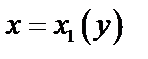 и
и 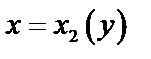
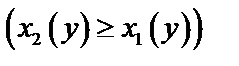 , каждая из которых пересекается прямой, параллельной оси
, каждая из которых пересекается прямой, параллельной оси 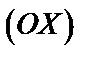 , только в одной точке (рис. 8).
, только в одной точке (рис. 8).
Для данной области двойной интеграл вычисляется по формуле:
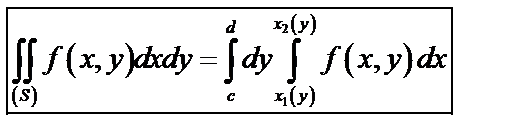 , (41)
, (41)
причем сначала вычисляется интеграл 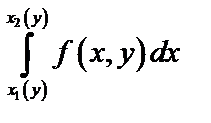 , в котором переменная
, в котором переменная 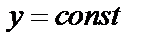 .
.
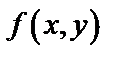 определена в ограниченной замкнутой области (S) плоскости (XOY).
определена в ограниченной замкнутой области (S) плоскости (XOY).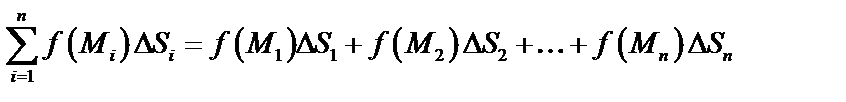 ,
,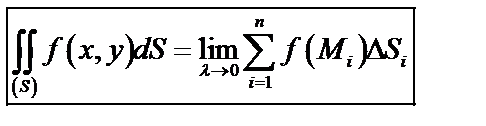 ,
,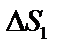 ,
, 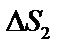 , …,
, …, 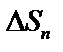 – площади частичных областей,
– площади частичных областей,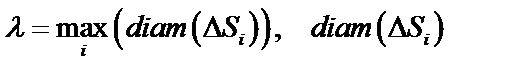 – диаметр
– диаметр 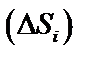 ,
,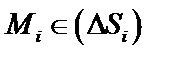 элементарной области.
элементарной области.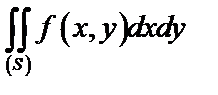 .
.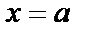 и
и 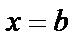
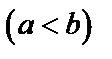 , а снизу и сверху – непрерывными кривыми
, а снизу и сверху – непрерывными кривыми 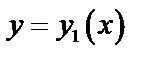 и
и 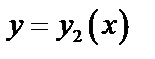
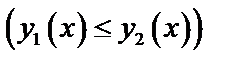 , каждая из которой пересекается прямой, параллельной оси
, каждая из которой пересекается прямой, параллельной оси 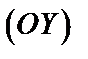 , только в одной точке (рис. 7).
, только в одной точке (рис. 7).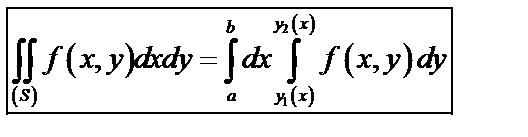 , (40)
, (40)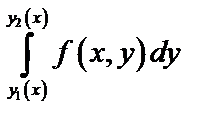 , где
, где 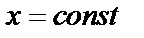 .
.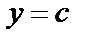 и
и 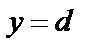
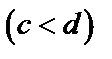 , а слева и справа – непрерывными кривыми
, а слева и справа – непрерывными кривыми 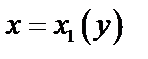 и
и 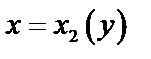
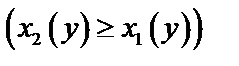 , каждая из которых пересекается прямой, параллельной оси
, каждая из которых пересекается прямой, параллельной оси 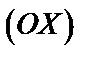 , только в одной точке (рис. 8).
, только в одной точке (рис. 8).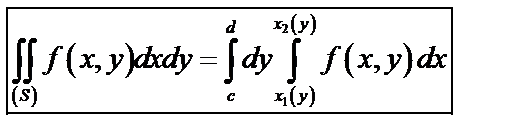 , (41)
, (41)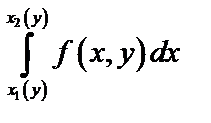 , в котором переменная
, в котором переменная 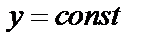 .
. 2015-05-13
2015-05-13 463
463








