Преобразование двойного интеграла от прямоугольных координат 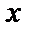 ,
, 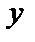 к полярным координатам
к полярным координатам 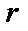 ,
, 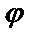 , связанными с прямоугольными координатами соотношениями
, связанными с прямоугольными координатами соотношениями 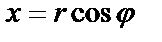 и
и 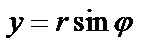 , осуществляется по формуле:
, осуществляется по формуле:
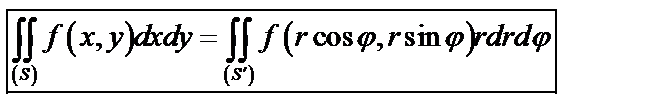 . (42)
. (42)
Если область интегрирования 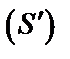 задана в виде:
задана в виде:
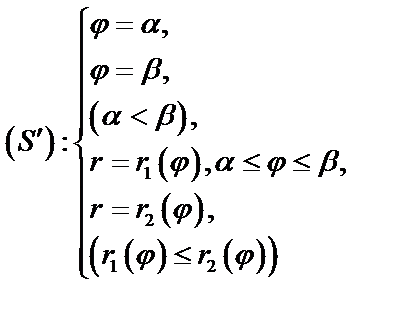
т.е. 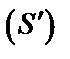 – ограничена двумя лучами
– ограничена двумя лучами 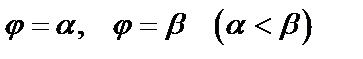 , выходящими из полюса, и двумя кривыми
, выходящими из полюса, и двумя кривыми 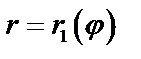 и
и 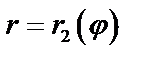 , где
, где 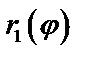 и
и 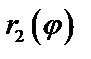 – однозначные функции при
– однозначные функции при 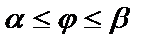 и
и 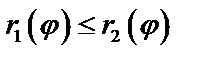 , то двойной интеграл вычисляется по формуле:
, то двойной интеграл вычисляется по формуле:
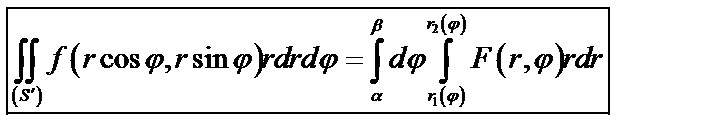 , (43)
, (43)
причем сначала вычисляется интеграл 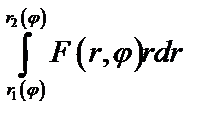 , где переменная
, где переменная 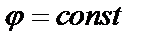 .
.
3.3. Вычисление площади плоской фигуры.
Площадь плоской фигуры, ограниченной областью 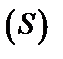 , находится по формуле:
, находится по формуле: 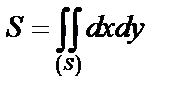 .
.
Если
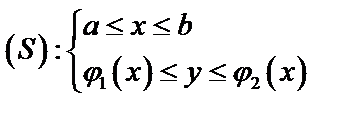 , то
, то 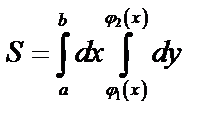 .
.
Если область 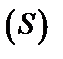 в полярных координатах определена неравенствами:
в полярных координатах определена неравенствами: 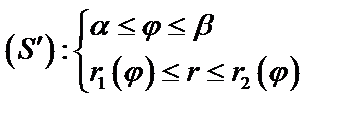 , то
, то 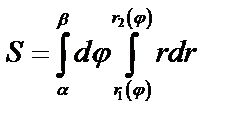 .
.
 2015-05-13
2015-05-13 410
410








