Положение произвольной точки М в сферических координатах определяется тройкой чисел: 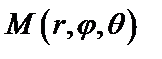 , где
, где
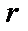 – расстояние точки М от начала координат,
– расстояние точки М от начала координат,
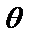 – угол между радиус-вектором точки М и положительным направлением оси
– угол между радиус-вектором точки М и положительным направлением оси 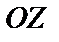 ,
,
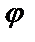 – угол между проекцией радиус-вектора точки М на плоскость
– угол между проекцией радиус-вектора точки М на плоскость 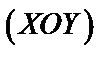 и положительным направлением оси
и положительным направлением оси 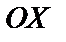 . (рис. 10)
. (рис. 10)
| y |
| x |
| z |
| r |
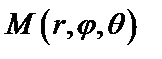
|
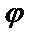
|
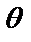
|
| Рис. 10 |
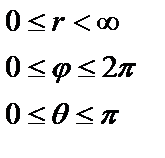
Связь с декартовыми координатами:
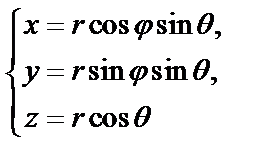
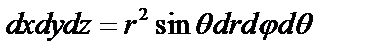 .
.
Тройной интеграл в сферических координатах имеет вид: 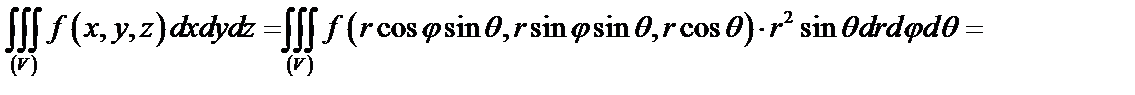
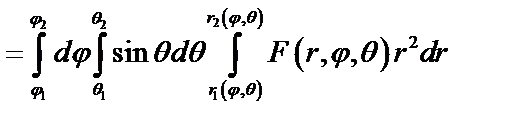 . (46)
. (46)
Приложения двойного и тройного интеграла.
1. Вычисление площади посредством двойного интеграла.
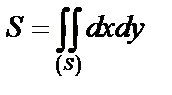 в прямоугольных координатах
в прямоугольных координатах
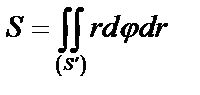 в полярных координатах. (47)
в полярных координатах. (47)
2. Вычисление объема тела посредством двойного интеграла
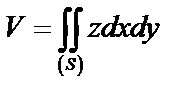
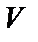 – объем вертикального цилиндрического тела, имеющего своим основанием область
– объем вертикального цилиндрического тела, имеющего своим основанием область 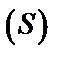 на плоскости
на плоскости 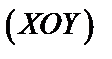 и ограниченного сверху поверхностью
и ограниченного сверху поверхностью 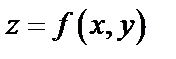 .
.
3. Вычисление массы, центра тяжести и момента инерции посредством двойного интеграла.
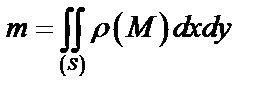 ,
, 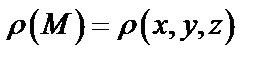 .
.
где 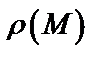 – поверхностная плотность в точке
– поверхностная плотность в точке 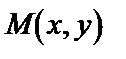 плоской фигуры (материальной пластинки), занимающей область
плоской фигуры (материальной пластинки), занимающей область 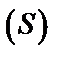 , а
, а 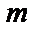 – масса материальной пластинки.
– масса материальной пластинки.
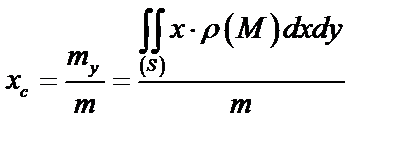 ;
;
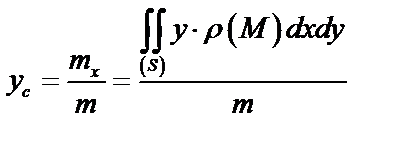 ,
,
где 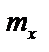 ,
, 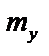 – статические моменты пластинки относительно осей
– статические моменты пластинки относительно осей 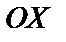 и
и 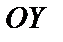 . Если пластинка однородна, то
. Если пластинка однородна, то 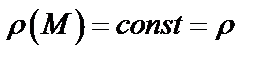 выносится за знаки интегралов и сокращается;
выносится за знаки интегралов и сокращается;
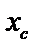 ,
, 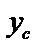 – координаты центра тяжести С.
– координаты центра тяжести С.
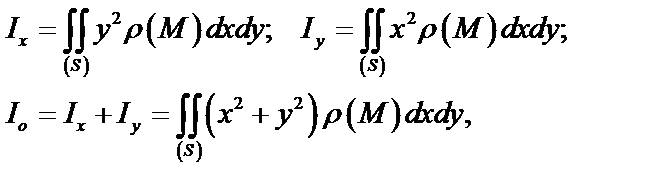
где 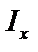 ,
, 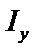 ,
, 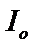 – моменты инерции относительно осей
– моменты инерции относительно осей 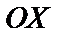 и
и 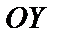 и начала координат О.
и начала координат О.
4. Вычисление объема пространственной области 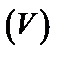 посредством тройного интеграла.
посредством тройного интеграла.
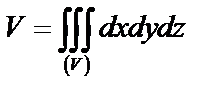
5. Вычисление массы тела, занимающего область 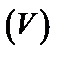 .
.
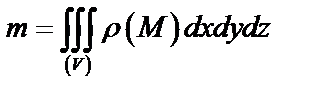 ,
,
где 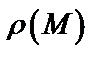 – объемная плотность распределения масса в точке
– объемная плотность распределения масса в точке 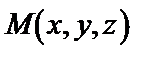 тела.
тела.
6. Вычисление координат центра тяжести С тела.
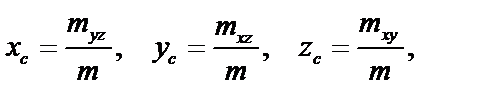
где 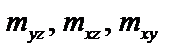 – статические моменты тела относительно координатных плоскостей:
– статические моменты тела относительно координатных плоскостей:
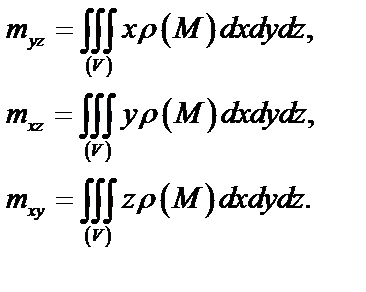
Для однородного тела 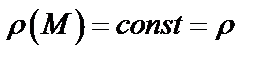 выносится за знаки и сокращается.
выносится за знаки и сокращается.
7. Вычисление моментов инерции тела относительно осей 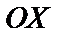 ,
, 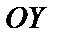 ,
, 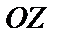 и начала координат О.
и начала координат О.
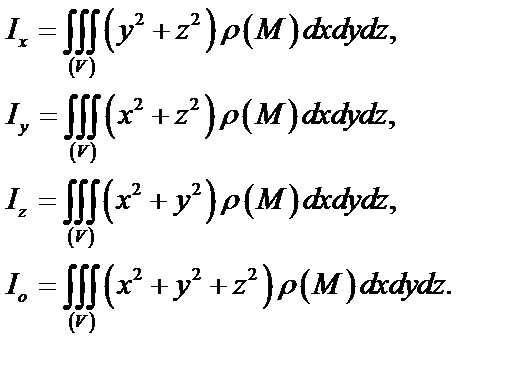
 2015-05-13
2015-05-13 446
446








