Вычисление криволинейного интеграла I рода

Пусть функция 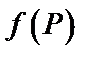определена и непрерывна в точках дуги 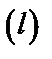гладкой кривой. Интегральной суммой для функции 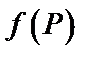по длине дуги 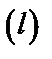называется сумма вида:

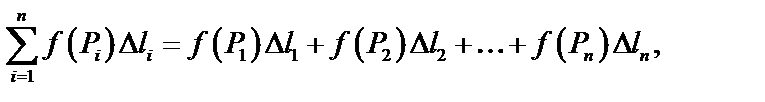
тогда криволинейный интеграл I рода:

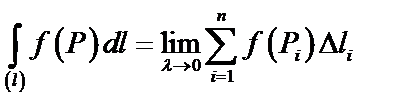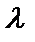, – шаг разбиения кривой .

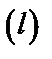Чтобы вычислить криволинейный интеграл I рода необходимо преобразовать его к определенному.

Для этого выражение, стоящее под знаком интеграла, нужно выразить через одну переменную, используя для этого уравнения линии.

Пусть 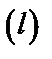– линия на плоскости.

а) ,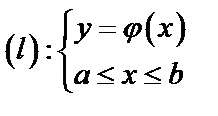

где функция 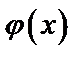дифференцируема на ,

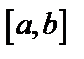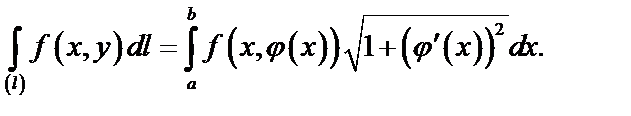
б) ,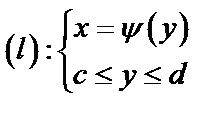

где функция 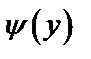дифференцируема на ,

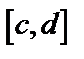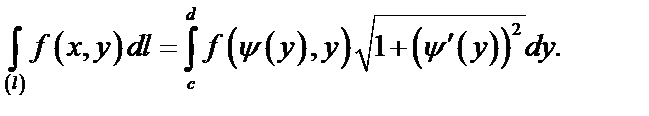
в)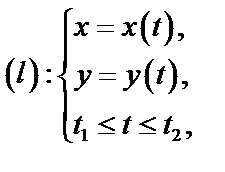

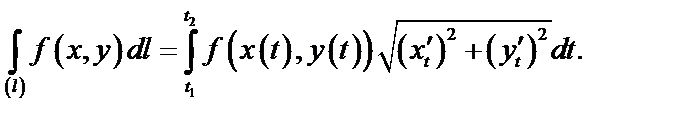
г) ,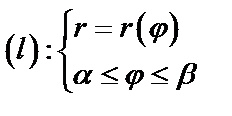

.

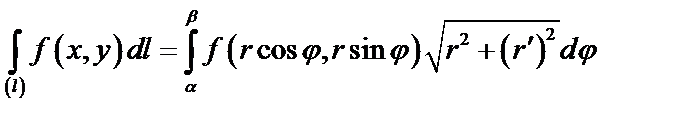Пусть 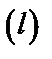– пространственная кривая, т.е.

,

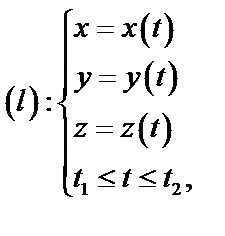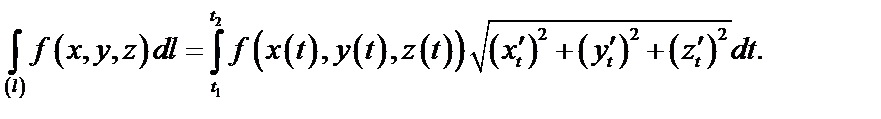
Если 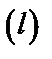– плоская (пространственная) кривая с линейной плотностью вещества в точке 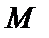: 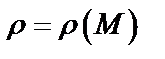, то массу материальной кривой 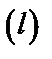находят по формлуле 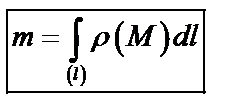(48)