Пусть 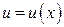 и
и 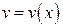 непрерывно дифференцируемые функции от
непрерывно дифференцируемые функции от 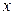 . Тогда
. Тогда
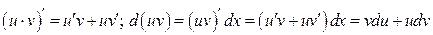 .
.
Напомним: если 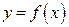 , то дифференциал
, то дифференциал 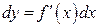 ; поэтому
; поэтому 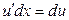 ;
; 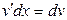 .
.
Тогда 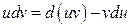 и
и 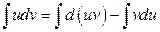 .
.
Учитывая, что 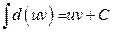 , получаем:
, получаем:
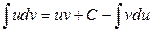 . (2.1)
. (2.1)
Поскольку в равенстве (2.1 справа стоит неопределенный интеграл, который также содержит произвольную постоянную, то постоянную 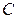 обычно опускают, и формулу интегрирования по частям записывают в виде
обычно опускают, и формулу интегрирования по частям записывают в виде
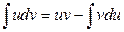 . (2.2)
. (2.2)
Эта формула применяется чаще всего к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей 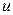 и
и 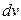 , чтобы нахождение функции
, чтобы нахождение функции 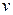 по ее дифференциалу
по ее дифференциалу 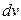 по формуле
по формуле 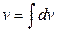 и вычисление
и вычисление 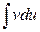 составили в совокупности задачу более простую, чем непосредственное вычисление
составили в совокупности задачу более простую, чем непосредственное вычисление 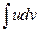 .
.
Укажем некоторые типы интегралов, которые находятся интегрированием по частям.
І. 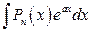 ;
; 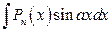 ;
; 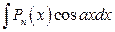 .
.
Здесь полагают 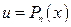 , а остальное включают в
, а остальное включают в 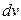 , т.е.
, т.е. 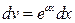 или
или 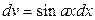 или
или 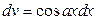 .
.
ІІ. 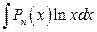 ;
; 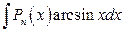 ;
; 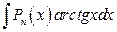 .
.
Здесь полагают 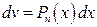 , а остальное включают в
, а остальное включают в 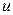 , т.е.
, т.е. 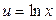 или
или 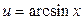 или
или 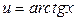 .
.
ІІІ. 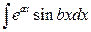 ;
; 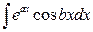 .
.
Здесь не имеет значения, что принимать за 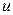 , а что включать в
, а что включать в 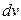 .
.
В приведенных интегралах 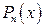 многочлен степени
многочлен степени 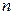 , т.е.
, т.е.
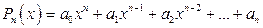 .
.
► Запишите формулу интегрирования по частям.
► Приведите примеры интегралов, которые относятся к І, ІІ, и ІІІ типу и укажите, что в них следует принять в качестве 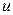 , а что включить в
, а что включить в 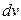 .
.
Пример 2.2. Найти неопределенные интегралы.
а) 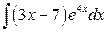 ; b)
; b) 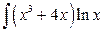 .
.
Решение:
а) интеграл относится к типу І, 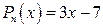 .
.
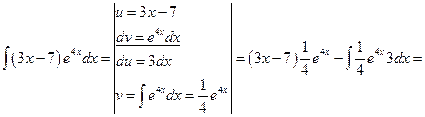
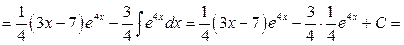
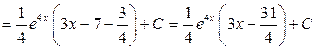 .
.
Замечание: при определении функции 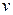 по ее дифференциалу
по ее дифференциалу 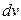 по свойству 2 неопределенного интеграла следует добавлять постоянную
по свойству 2 неопределенного интеграла следует добавлять постоянную 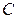 , но т.к. в конечный результат она не входит (что легко проверить, подставив в равенстве (2.2) вместо
, но т.к. в конечный результат она не входит (что легко проверить, подставив в равенстве (2.2) вместо 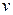 выражение
выражение 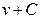 ), то удобно считать произвольную постоянную
), то удобно считать произвольную постоянную 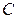 равной нулю;
равной нулю;
b) второй интеграл относится к типу ІІ, 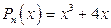 .
.
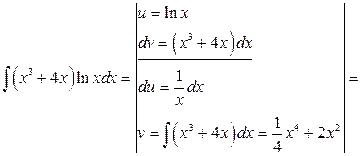
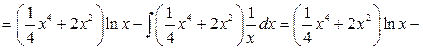
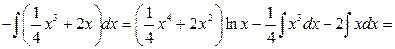
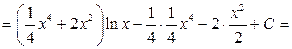
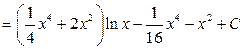 .
.
▶ Найти 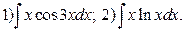
Ответы: 1) 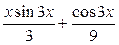 ; 2)
; 2) 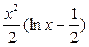 .
.
 2015-05-13
2015-05-13 416
416








