Пусть требуется найти 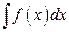 , причем непосредственным интегрированием это не удается.
, причем непосредственным интегрированием это не удается.
Сделаем замену переменной в подинтегральном выражении, положив
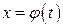 , (2.3)
, (2.3)
где 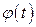 - непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда
- непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда 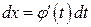 и справедливо равенство
и справедливо равенство
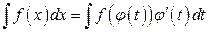 . (2.4)
. (2.4)
Подчеркнем, что после нахождения интеграла в (2.4) следует в полученный результат подставить вместо 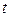 его выражение через
его выражение через 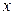 , найденное из равенства (2.3).
, найденное из равенства (2.3).
Удачный выбор новой переменной существенно облегчает нахождение интеграла.
При этом помогут следующие соображения: если подынтегральное выражение содержит функции 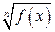 ,
, 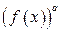 ,
, 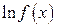 ,
, 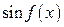 ,
, 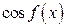 ,
, 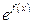 ,
, 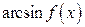 ,
, 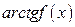 , у которых вместо
, у которых вместо 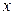 аргументом является
аргументом является  , как правило, применяется подстановка
, как правило, применяется подстановка 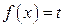 . Если подынтегральное выражение содержит корни разных степеней из одного и того же выражения, то это выражение и принимается за новую переменную
. Если подынтегральное выражение содержит корни разных степеней из одного и того же выражения, то это выражение и принимается за новую переменную 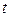 в такой степени, чтобы все корни «извлекались».
в такой степени, чтобы все корни «извлекались».
Пример 2.3. Найти интегралы
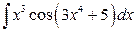 ,
, 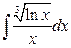 ,
, 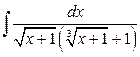 .
.
 2015-05-13
2015-05-13 340
340








