Пусть 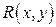 - рациональная функция своих аргументов
- рациональная функция своих аргументов 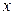 и
и 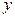 , т.е. над
, т.е. над 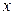 и
и 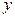 совершаются только арифметические операции. Например,
совершаются только арифметические операции. Например,
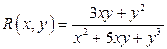 ;
; 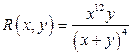 .
.
Функция 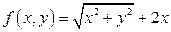 не является рациональной.
не является рациональной.
Универсальная подстановка.
Интеграл вида 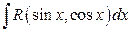 с помощью подстановки
с помощью подстановки 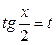 , которая называется универсальной, всегда сводится к интегралу от рациональной функции от переменной
, которая называется универсальной, всегда сводится к интегралу от рациональной функции от переменной 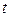 .
.
Действительно, 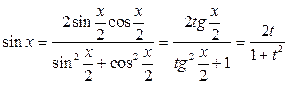 ,
,
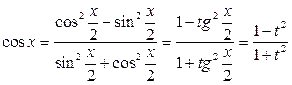 ,
,
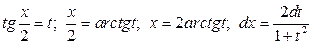 .
.
Поэтому 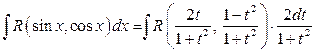 , т.е. получим интеграл от рациональной функции по переменной
, т.е. получим интеграл от рациональной функции по переменной 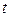 (т.е., как говорят, рационализируем интеграл).
(т.е., как говорят, рационализируем интеграл).
Пример 2.7. Найти 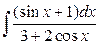 , применив универсальную подстановку.
, применив универсальную подстановку.
 2015-05-13
2015-05-13 271
271








