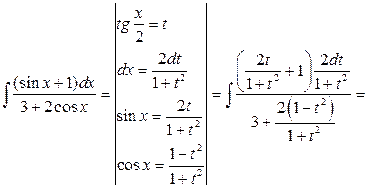
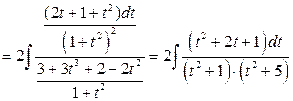 .
.
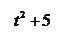
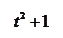 Разложим полученную рациональную правильную дробь на сумму простейших дробей, учитывая, что знаменатель имеет только комплексные корни (
Разложим полученную рациональную правильную дробь на сумму простейших дробей, учитывая, что знаменатель имеет только комплексные корни (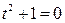 ;
; 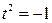 ;
; 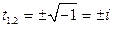 ;
; 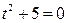 ;
; 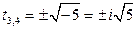 ).
).
 |  |
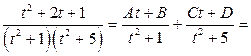
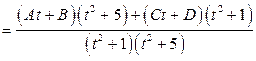 .
.
Приравниваем числители:
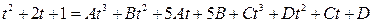 .
.
Приведем подобные в правой части равенства:
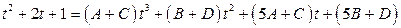 .
.
Для определения коэффициентов 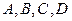 применим метод приравнивания коэффициентов при одинаковых степенях
применим метод приравнивания коэффициентов при одинаковых степенях 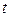 :
:

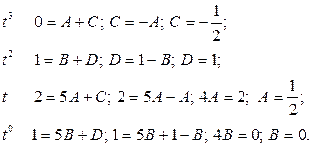
Заметим, что полученная система четырех уравнений распалась на две системы двух уравнений 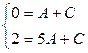 и
и 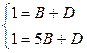 , которые и были решены.
, которые и были решены.
Учитывая полученные результаты для 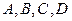 , можно записать:
, можно записать:
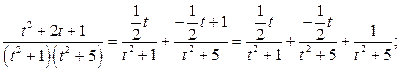
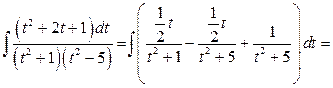
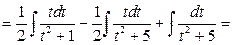
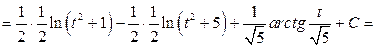
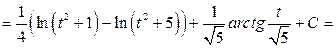
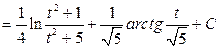 .
.
Вспомогательные вычисления:
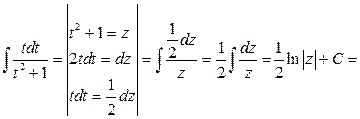
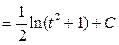 .
.
Аналогично находится 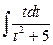 .
.
Таким образом, 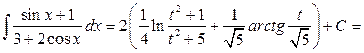
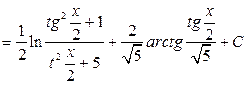 .
.
Применение универсальной подстановки, как правило, приводит к громоздким вычислениям, о чем свидетельствует и решение примера (2.7). Поэтому ниже приведем частные случаи, когда интеграл можно рационализировать, не применяя универсальную подстановку, что упрощает вычисления.
1. 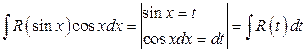 .
.
2. 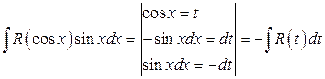 .
.
3. 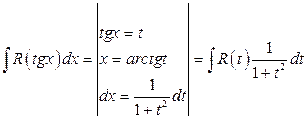 .
.
4. 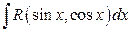 при условии, что
при условии, что 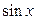 и
и 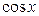 входят в подынтегральную функцию только в четных степенях, рационализируется также подстановкой
входят в подынтегральную функцию только в четных степенях, рационализируется также подстановкой 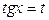 , поскольку
, поскольку 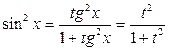 ,
, 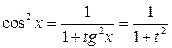 .
.
5. 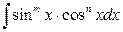 рационализируется: подстановкой
рационализируется: подстановкой 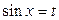 , если
, если 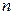 -нечетное, подстановкой
-нечетное, подстановкой 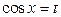 , если
, если 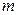 - нечетное; применением формул
- нечетное; применением формул 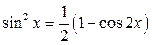 ,
, 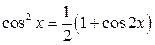 , если
, если 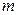 и
и 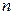 - неотрицательные четные числа; если
- неотрицательные четные числа; если 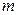 и
и 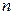 - четные числа, но хотя бы одно отрицательное, то подстановкой
- четные числа, но хотя бы одно отрицательное, то подстановкой 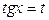 (случай 4).
(случай 4).
6. 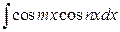 ,
, 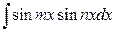 ,
, 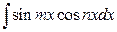 вычисляются применением формул
вычисляются применением формул 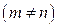
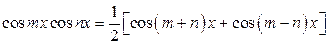 ,
,
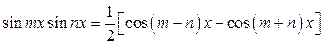 ,
,
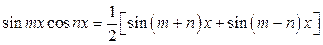
и таблицы интегралов.
► Представьте в виде суммы (разности) выражения 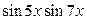 ,
, 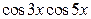 ,
, 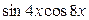 .
.
► Приведите примеры интегралов, которые соответствовали бы пунктам 1-6, и укажите подстановку, с помощью которой их можно рационализировать.
Пример 2.8. Найти интегралы от выражений, содержащих тригонометрические функции.
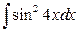 ,
, 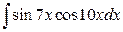 ,
, 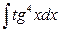 .
.
 2015-05-13
2015-05-13 388
388








