1) Воспользуемся формулой 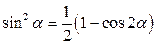 .
.
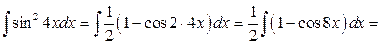
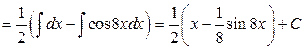 .
.
2) В соответствии с формулой
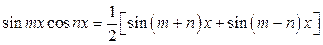 ,
,
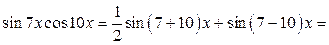
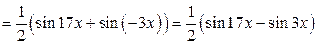 .
.
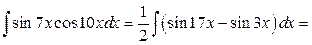
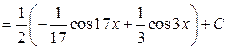 .
.
3) 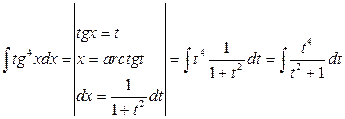 .
.
Получим интеграл от неправильной рациональной дроби. В данной ситуации выделить целую часть можно следующим образом:
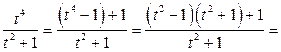
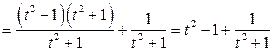 ,
,
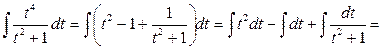
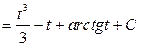 .
.
Следовательно,
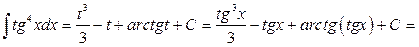
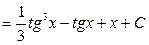 .
.
▶ Найти интегралы от выражений, содержащих тригонометрические функции.
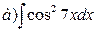 ,
, 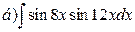 ,
, 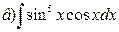 ,
, 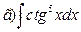 .
.
В последнем интеграле следует применить подстановку 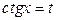 ,
, 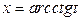 ,
, 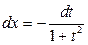 .
.
Ответы: а) 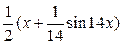 ; б)
; б) 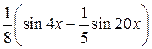 ;
;
в) 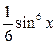 ; г)
; г) 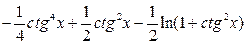 .
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
 2015-05-13
2015-05-13 429
429








