Пусть на отрезке 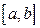 задана ограниченная функция
задана ограниченная функция  . Разделим отрезок
. Разделим отрезок 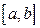 произвольным образом на
произвольным образом на 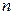 частей
частей 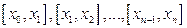 точками
точками 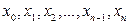
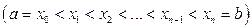 . На каждом частичном отрезке
. На каждом частичном отрезке 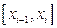 разбиения выберем произвольную точку
разбиения выберем произвольную точку 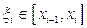 , вычислим в ней значение функции
, вычислим в ней значение функции 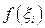 , умножим его на длину отрезка
, умножим его на длину отрезка 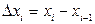 и составим сумму
и составим сумму
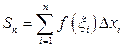 ,
,
которую называют интегральной сумой функции  , соответствующей выбранному разбиению.
, соответствующей выбранному разбиению.
Предел, к которому стремится интегральная сумма 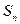 , когда максимальная из длин частичных отрезков стремится к нулю, если он существует и не зависит ни от способа разбиения отрезка
, когда максимальная из длин частичных отрезков стремится к нулю, если он существует и не зависит ни от способа разбиения отрезка 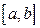 , ни от выбора точек
, ни от выбора точек 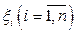 , называется определенным интегралом от функции
, называется определенным интегралом от функции  на отрезке
на отрезке 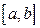 и обозначается символом
и обозначается символом 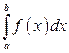 .
.
Таким образом, по определению
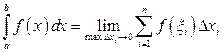 (3.1)
(3.1)
Число 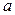 называется нижним пределом, а
называется нижним пределом, а 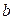 - верхним пределом определенного интеграла; отрезок
- верхним пределом определенного интеграла; отрезок 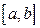 называется отрезком интегрирования,
называется отрезком интегрирования, 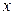 - переменной интегрирования.
- переменной интегрирования.
Если для функции  предел (3.1) существует, то она называется интегрируемой на отрезке
предел (3.1) существует, то она называется интегрируемой на отрезке 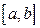 .
.
Имеет место утверждение: если функция  непрерывна на отрезке
непрерывна на отрезке 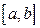 , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
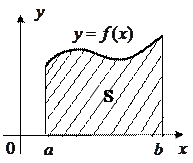 Геометрический смысл определенного интеграла: если
Геометрический смысл определенного интеграла: если 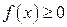 на отрезке
на отрезке 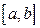 , то
, то 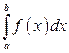 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 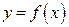 , прямыми
, прямыми 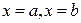 и осью
и осью 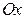 (рис.3.1):
(рис.3.1):
.
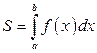
Рис. 3.1.
Отметим, что, по определению,
1) 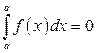 ; 2)
; 2) 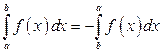 . (3.2)
. (3.2)
Приведем без доказательства основные свойства определенного интеграла, часть из которых проиллюстрируем графически, пользуясь геометрическим смыслом определенного интеграла.
- Постоянный множитель можно выносить за знак определенного интеграла
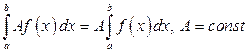 .
.
- Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от слагаемых функций.
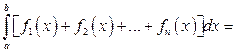
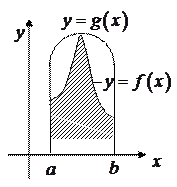
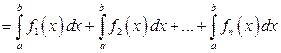 .
.
- Если на отрезке
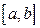 , где
, где 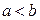 , функции
, функции  и
и 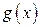 удовлетворяют условию
удовлетворяют условию
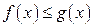 , то
, то 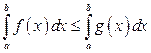
 Рис. 3.2
Рис. 3.2
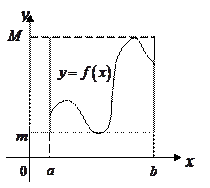
Рис.3.3.
4. Если 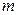 и
и 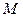 - наименьшее и наибольшее значения функции
- наименьшее и наибольшее значения функции  на отрезке
на отрезке 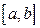 и
и 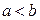 , то
, то 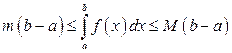
5. Если функция  непрерывна на отрезке
непрерывна на отрезке 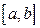 , то на этом отрезке существует такая точка
, то на этом отрезке существует такая точка 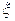 , что справедливо равенство
, что справедливо равенство
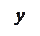
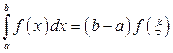 .
.
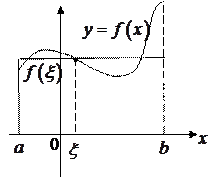 |
Рис.3.4.



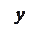 6. Если функция
6. Если функция  интегрируема на каждом из отрезков
интегрируема на каждом из отрезков 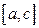 и
и 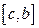 , то она интегрируема и на отрезке
, то она интегрируема и на отрезке 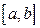 и
и 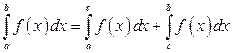
Рис.3.5.
- Если подынтегральная функция
 четная (
четная (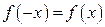 ) на отрезке интегрирования
) на отрезке интегрирования 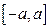 , то
, то 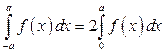 .
.
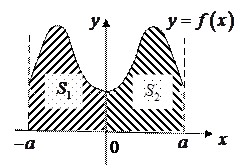 |
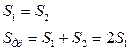
Рис.3.6.
8. Если подынтегральная функция  нечетная (
нечетная (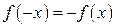 ) на отрезке интегрирования
) на отрезке интегрирования 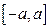 , то
, то 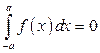 .
.
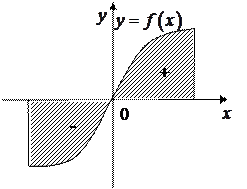
Рис.3.7.
9. Если подынтегральная функция  - периодическая с периодом
- периодическая с периодом 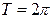 (
(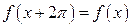 ), то
), то 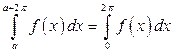 , т.е. для периодической с периодом
, т.е. для периодической с периодом 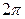 функции определенный интеграл дает одно и то же значение при интегрировании по любому отрезку длиной, равной
функции определенный интеграл дает одно и то же значение при интегрировании по любому отрезку длиной, равной 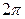 .
.
► Запишите формулировку свойств определенного интеграла, записанных формулами (3.2).
► Запишите свойство 2) определенного интеграла для случая трех слагаемых функций.
 2015-05-13
2015-05-13 2074
2074
