При решении задач на динамику твердого тела, как правило, необходимо применять основное уравнение динамики вращательного движения. Часто в подобных задачах твердое тело приводится в движение силами натяжения нитей, к которым подвешены грузы, поэтому необходимо также записывать уравнения движения (второй закон Ньютона) для грузов. Условие, связывающее два типа движения, как правило, заключается в отсутствии проскальзывания нити, что позволяет получить кинематическую связь между линейным ускорением груза и угловым ускорением твердого тела. Рассмотрим конкретные примеры.
 |
Задача 1. Два тела, массы которых 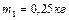 и
и 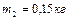 , связаны нитью, переброшенной через блок. Блок массой
, связаны нитью, переброшенной через блок. Блок массой 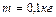 укреплен на краю горизонтального стола, по поверхности которого скользит тело массой
укреплен на краю горизонтального стола, по поверхности которого скользит тело массой 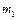 . Коэффициент трения тела
. Коэффициент трения тела 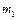 о поверхность стола
о поверхность стола 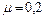 . С каким ускорением движутся тела и каковы силы натяжения нити по обе стороны от блока? Массу блока можно считать равномерно распределенной по ободу, трением в подшипниках оси блока пренебречь.
. С каким ускорением движутся тела и каковы силы натяжения нити по обе стороны от блока? Массу блока можно считать равномерно распределенной по ободу, трением в подшипниках оси блока пренебречь.
Решение
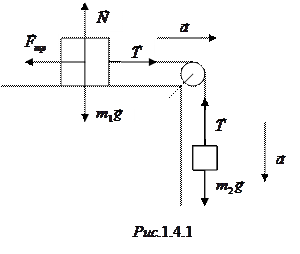
Применим для грузов второй закон Ньютона, а для блока – основное уравнение динамики вращательного движения. Силы, действующие на грузы, показаны на рис.1.4.1.
Для груза 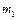 второй закон Ньютона в проекциях на горизонтальное и вертикальное направления принимает вид
второй закон Ньютона в проекциях на горизонтальное и вертикальное направления принимает вид
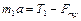 ,
, 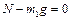 , (1.4.1)
, (1.4.1)
а по определению сила трения скольжения
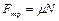 .
.
Для груза 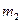 уравнение вертикального движения
уравнение вертикального движения
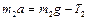 . (1.4.2)
. (1.4.2)
Наконец, уравнение вращательного движения блока
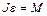 , (1.4.3)
, (1.4.3)
где 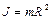 - момент инерции блока (обруча),
- момент инерции блока (обруча), 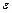 - угловое ускорение блока,
- угловое ускорение блока, 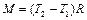 - результирующий момент сил натяжения, действующий на блок.
- результирующий момент сил натяжения, действующий на блок.
При отсутствии скольжения нити по блоку его угловое ускорение связано с линейным ускорением грузов по формуле 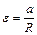 . С учетом приведенных соотношений уравнение (1.4.3) принимает вид
. С учетом приведенных соотношений уравнение (1.4.3) принимает вид
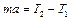 . (1.4.4)
. (1.4.4)
Исключая из (1.4.1) силы трения и реакции опоры, получаем
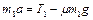 . (1.4.5)
. (1.4.5)
Наконец, складывая уравнения (1.4.2), (1.4.4), (1.4.5), получаем
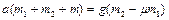 ,
,
откуда находим
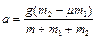 . (1.4.6)
. (1.4.6)
Подставляя числовые значения, получаем
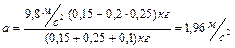 .
.
Подставляя (1.4.6) в (1.4.2) и (1.4.5), находим силы натяжения:
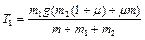 ,
,
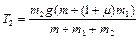 .
.
Вычисления приводят к результатам:
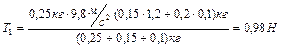 ,
, 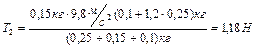 .
.
Задача 2. В однородном диске массой 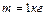 и радиусом
и радиусом 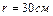 вырезано круглое отверстие диаметром
вырезано круглое отверстие диаметром 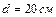 , центр которого находится на расстоянии
, центр которого находится на расстоянии 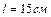 от оси диска. Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
от оси диска. Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
Решение
Данное тело можно представить как совокупность сплошного диска, изготовленного из материала с некоторой плотностью, и другого диска из материала с такой же по величине, но противоположной по знаку плотностью, расположенного в отверстии первого диска. Тогда результирующий момент инерции этой системы можно найти, вычитая из момента инерции первого диска момент инерции второго диска.
Для первого диска
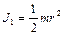 ,
,
а для второго по теореме Штейнера
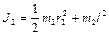 ,
,
где 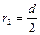 , а массу второго диска можно определить из условия пропорциональности массы и площади:
, а массу второго диска можно определить из условия пропорциональности массы и площади: 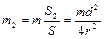 .
.
Тогда 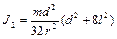 , следовательно,
, следовательно,
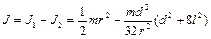 .
.
Выполняя вычисления, находим
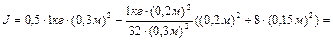 .
.
 |
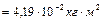 .
. Задача 3. Однородный тонкий стержень массой 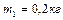 и
и
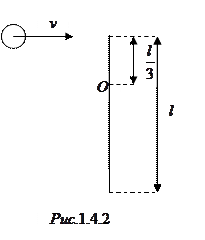
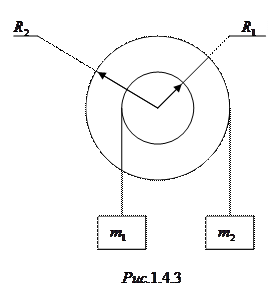
длиной 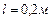 может свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис.1.4.2). В верхний конец стержня попадает пластилиновый шарик массой
может свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис.1.4.2). В верхний конец стержня попадает пластилиновый шарик массой 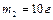 , движущийся со скоростью
, движущийся со скоростью 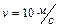 , и прилипает к стержню. Определить угловую скорость стержня и линейную скорость нижнего конца стержня сразу после удара, если расстояние от верхнего конца стержня до точки О равно
, и прилипает к стержню. Определить угловую скорость стержня и линейную скорость нижнего конца стержня сразу после удара, если расстояние от верхнего конца стержня до точки О равно 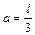 .
.
Решение
Для определения угловой скорости вращения стержня воспользуемся законом сохранения момента импульса. Рассматривая шарик как материальную точку, получаем:
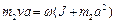 , (1.4.7)
, (1.4.7)
где момент инерции стержня относительно точки О по теореме Штейнера равен
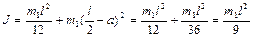 . (1.4.8)
. (1.4.8)
Из (1.4.7) и (1.4.8) находим угловую скорость стержня сразу после удара
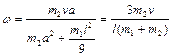 .
.
Вычисления дают
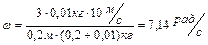 .
.
Для определения линейной скорости нижнего конца стержня воспользуемся связью линейной и угловой скорости: 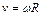 , где радиус окружности равен
, где радиус окружности равен 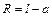 . Получаем
. Получаем
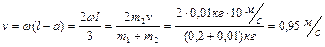 .
.
 |
Задача 4. На ступенчатый цилиндрический блок намотаны в противоположных направлениях две нити с подвешенными к ним грузами массами
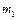 и
и 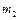 (рис.1.4.3). Найти ускорения грузов и силы натяжения нитей. Момент инерции блока
(рис.1.4.3). Найти ускорения грузов и силы натяжения нитей. Момент инерции блока 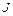 , радиусы соответствующих участков блока
, радиусы соответствующих участков блока 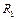 и
и 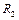 .
. Решение
Запишем второй закон Ньютона для грузов в проекции на вертикальное направление
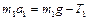 ,
, 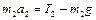 , (1.4.9)
, (1.4.9)
где 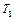 и
и 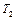 - силы натяжения нитей.
- силы натяжения нитей.
Уравнение вращательного движения блока
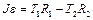 . (1.4.10)
. (1.4.10)
В силу отсутствия проскальзывания нитей по блоку можно записать
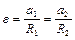 . (1.4.11)
. (1.4.11)
Из (1.4.9) – (1.4.11) следует
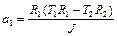 ,
, 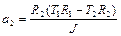 . (1.4.12)
. (1.4.12)
Подставляя в уравнения движения грузов, получаем систему уравнений для определения сил натяжения нитей
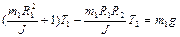 ,
,
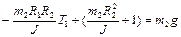 . (1.4.13)
. (1.4.13)
Решая систему (1.4.13), находим
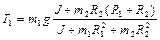 ,
, 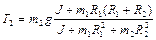 .
.
Подстановка полученных результатов в (1.4.12) дает
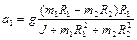 ,
, 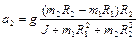 .
.
Задача 5. Два диска с моментами инерции 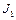 и
и 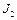 вращаются с угловыми скоростями
вращаются с угловыми скоростями 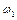 и
и 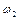 вокруг одной и той же оси без трения. Диски пришли в соприкосновение друг с другом. Из-за возникшего между дисками трения через некоторое время проскальзывание одного диска по другому прекращается. Какова станет тогда угловая скорость вращения дисков? Какое количество теплоты выделится?
вокруг одной и той же оси без трения. Диски пришли в соприкосновение друг с другом. Из-за возникшего между дисками трения через некоторое время проскальзывание одного диска по другому прекращается. Какова станет тогда угловая скорость вращения дисков? Какое количество теплоты выделится?
Решение
Применим закон сохранения момента импульса. Получаем
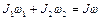 ,
,
где 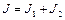 - момент инерции системы,
- момент инерции системы, 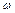 - угловая скорость системы после прекращения проскальзывания. В результате находим
- угловая скорость системы после прекращения проскальзывания. В результате находим
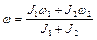 .
.
Для определения количества теплоты, выделившегося в результате взаимодействия дисков, воспользуемся законом сохранения энергии, согласно которому
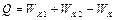 ,
,
где 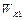 и
и 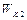 - кинетические энергии дисков до взаимодействия,
- кинетические энергии дисков до взаимодействия, 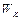 - кинетическая энергия системы после взаимодействия. Поскольку
- кинетическая энергия системы после взаимодействия. Поскольку
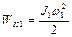 ,
, 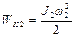 ,
, 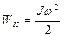 ,
,
получаем
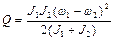 .
.
Задача 6. Тонкий обруч радиуса 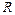 раскрутили вокруг его оси до угловой скорости
раскрутили вокруг его оси до угловой скорости 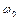 и положили плашмя на горизонтальный стол. Через какое время обруч остановится, если коэффициент трения между столом и обручем равен
и положили плашмя на горизонтальный стол. Через какое время обруч остановится, если коэффициент трения между столом и обручем равен 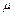 ? Сколько оборотов сделает обруч до полной остановки?
? Сколько оборотов сделает обруч до полной остановки?
Решение
Так как действующая на обруч сила трения постоянна, то вращение обруча будет равнозамедленным, и мы можем применить уравнения равнозамедленного вращения
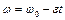 ,
, 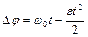 .
.
Если обруч сделает до остановки 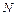 оборотов, то угол поворота составит
оборотов, то угол поворота составит 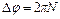 . В момент остановки обруча угловая скорость
. В момент остановки обруча угловая скорость 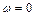 , следовательно,
, следовательно,
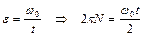 . (1.4.14)
. (1.4.14)
Воспользуемся законом сохранения энергии, согласно которому работа силы трения равна изменению кинетической энергии обруча
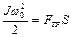 . (1.4.15)
. (1.4.15)
Здесь 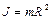 - момент инерции обруча,
- момент инерции обруча, 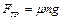 - сила трения и
- сила трения и 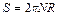 - путь, пройденный каждой точкой обруча до его остановки.
- путь, пройденный каждой точкой обруча до его остановки.
Решая систему уравнений (1.4.14), (1.4.15) с учетом выписанных соотношений для пути, силы трения и момента инерции, получаем
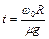 ,
, 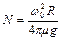 .
.
 2015-05-13
2015-05-13 15289
15289
