Пример 7.1: Кривая проходит через точку (1;2) и обладает тем свойством, что отношение ординаты любой ее точки к абсциссе пропорционально угловому коэффициенту касательной к этой кривой проведенной в этой же точке с коэффициентом пропорциональности к=3 составит дифференциальное уравнение (рис.11.2).
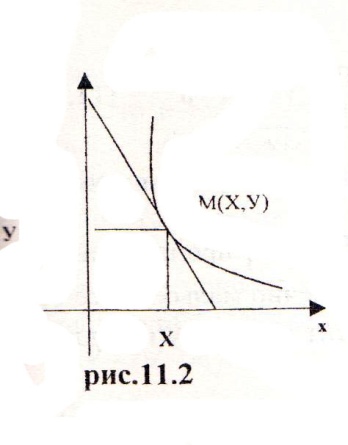 Решение: Пусть М(х,у) произвольная точка, через которую проходит кривая у = у (х)
Решение: Пусть М(х,у) произвольная точка, через которую проходит кривая у = у (х)
По условию задачи
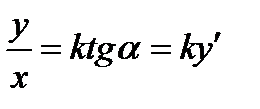
Так как по условию к=3, то уравнение (7.1) запишем в виде
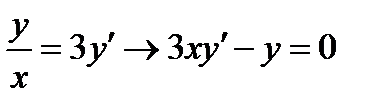 (7.9)
(7.9)
 Пример 7.2: Кривая проходит через точку (1;5) и обладает, тем свойством, что отрезок отсекаемый на оси ординат любой касательной, равен утроенной абсиссе точки касания. Найти уравнение кривой.
Пример 7.2: Кривая проходит через точку (1;5) и обладает, тем свойством, что отрезок отсекаемый на оси ординат любой касательной, равен утроенной абсиссе точки касания. Найти уравнение кривой.
Решение: Пусть М(х,у) –любая точка искомой кривой у = у (х) уравнение касательной в точке М(х,у) имеет 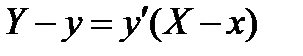
Где х,у –текущие координаты касательной. Пологая в этом уравнении х=0, находим
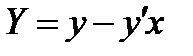
Так что ОВ: ОВ= 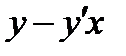
Условие задачи приводит к уравнению
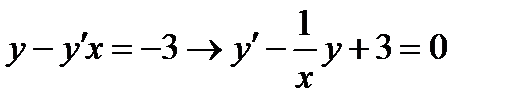 (7.10)
(7.10)
Пример7.3: Материальная точка массы m=1г движется прямолинейно, на нее действует в направлении движения сила, пропорциональная времени с коэффииентом к1=2*10-5 кг м/с, и сила сопротивления пропорциональная скорости, с коэффииентом к2= 0,003кг/с. Найти скорость точки через 3сек после начала движения, если начальная скорость 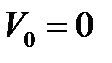 .
.
Решение: Пусть 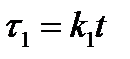
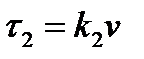
Тело движется под действием равнодействующих двух сил 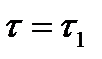 ,
, 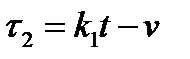
Дифферениальное уравнение движения запишется
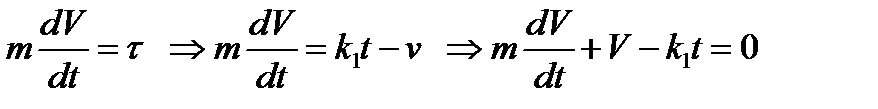 (7.11)
(7.11)
Пример 7.4: рассмотрим следующую задачу о текучести рабочей силы.
Пусть изменение ∆у числа рабочих за время 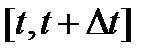 пропорционально с точностью до бесконечно малых более
пропорционально с точностью до бесконечно малых более 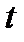 числу у(
числу у(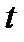 ) и длине рассматриваемого временного промежутка
) и длине рассматриваемого временного промежутка 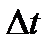 т.е
т.е
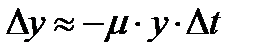 (7.12)
(7.12)
Знак минуса с права связан с тем, что мы рассматриваем задачу о текучести кадров, т.е 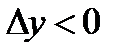 , следовательно знак в правой части должен быть тоже отрицательным. Равенство (7.12) приближенное потому, что в нем опущены бесконечно малые более высокого порядка малости по сравнению с
, следовательно знак в правой части должен быть тоже отрицательным. Равенство (7.12) приближенное потому, что в нем опущены бесконечно малые более высокого порядка малости по сравнению с 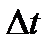 . Это в частности означает что чем меньше
. Это в частности означает что чем меньше 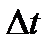 , тем точнее это приближенное равенство. Чтобы получить из приближенного равенства точное, нужно устремить
, тем точнее это приближенное равенство. Чтобы получить из приближенного равенства точное, нужно устремить 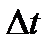 к нулю. Однако, если это сделать непосредственно в (7.12), то это не даст ничего, кроме тривиального равенства 0=0, не дающего никакой информации для определения искомой функции у(
к нулю. Однако, если это сделать непосредственно в (7.12), то это не даст ничего, кроме тривиального равенства 0=0, не дающего никакой информации для определения искомой функции у(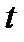 ). Поэтому поступим иначе. Разделим обе части в равенстве (7.12) на
). Поэтому поступим иначе. Разделим обе части в равенстве (7.12) на 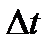 :
:
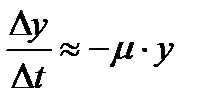
После чего перейдем к пределу при 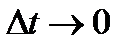 .
.
В пределе получим
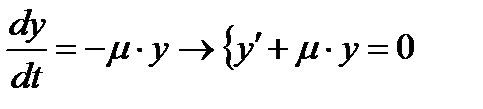 (7.13)
(7.13)
Пример 7.5: число рождений за момент времени 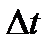 . И численности населения
. И численности населения 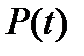 в момент времени
в момент времени 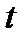 . Коэффициент пропорциональности обозначим через n; он измеряет рождаемость. Естественно, что этот коэффициент можно считать постоянным лишь в пределах такого интервала времени, в течении которого не происходит изменения условий, влияющих на рождаемость, также естественно, что этот коэффициент, вообще говоря, будет разным для разных регионов. Скажем, он в данный момент наибольшее значение имеет в Казахстане, а наименьший в Латвии и Эстонии.
. Коэффициент пропорциональности обозначим через n; он измеряет рождаемость. Естественно, что этот коэффициент можно считать постоянным лишь в пределах такого интервала времени, в течении которого не происходит изменения условий, влияющих на рождаемость, также естественно, что этот коэффициент, вообще говоря, будет разным для разных регионов. Скажем, он в данный момент наибольшее значение имеет в Казахстане, а наименьший в Латвии и Эстонии.
С другой стороны, наряду с рождением новых членов общества имеет место и такое печальное явление как смерть, в силу старости, болезней, несчастных случаев. Число этих явлений также пропорционально численности населения и промежутку времени 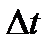 , коэффициент пропорциональности обозначим через m.
, коэффициент пропорциональности обозначим через m.
Рассуждая аналогично, как и в предыдущем примере, можем написать, что прирост населения 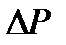 равен разности между числом родившихся
равен разности между числом родившихся 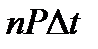 и числом
и числом 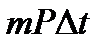 , т.е
, т.е
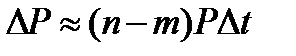
Откуда
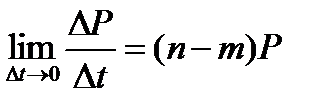
Т.е для неизвестной численности населения 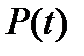 получим уравнение
получим уравнение
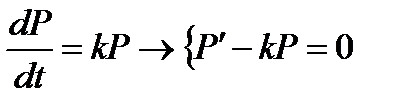 (7.14)
(7.14)
Где 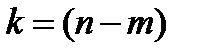
Пример 7.6: Следующий пример приведем из естествознания.
Рассмотрим явление радиоактивного распада. Закон радиоактивного распада, гласит, что изменение 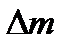 массы
массы 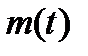 радиоактивного вещества пропорционально в промежуток
радиоактивного вещества пропорционально в промежуток 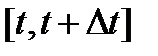 массе
массе 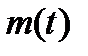 , длине промежутка
, длине промежутка 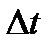 . Коэффициент обозначим через
. Коэффициент обозначим через 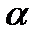 .
.
Имеем 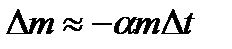
Откуда, рассуждая как и выше, получим уравнение
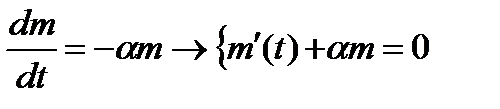 (7.15)
(7.15)
Таким образом мы пришли к понятию дифференциального уравнения.
Определение 7.1 Дифференциальным уравнением называется уравнение связывающее искомое функции у, и независимое переменное и ее производные от искомой функции.
Символически дифференциальное уравнение записывается в виде
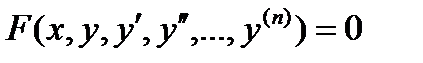 (
(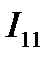 )
)
Здесь 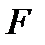 есть заданная функция от (n+2) переменных, удовлетворяющая определенным условиям непрерывности и дифференцируемости, а
есть заданная функция от (n+2) переменных, удовлетворяющая определенным условиям непрерывности и дифференцируемости, а 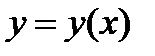 функция от х –решение дифференциального уравнения, которое надо найти.
функция от х –решение дифференциального уравнения, которое надо найти.
Определение 7.2 Порядком дифференциального уравнения называется наивысший порядок производных, входящих в данное уравнение.
В примерах (1-6) является дифференциальным уравнением первого порядка.
Уравнение вида
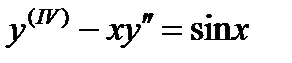
Является уравнением четвертого порядка.
Определение 7.3 Решением дифференциального уравнения порядка n называется функция 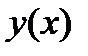 , имеющая на некотором интервале (а,б) производные
, имеющая на некотором интервале (а,б) производные 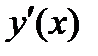 ,
, 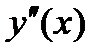 ,…,
,…, 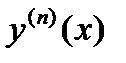 до n порядка включительно и удовлетворяющая этому уравнению.
до n порядка включительно и удовлетворяющая этому уравнению.
Это значит, что выполняется тождество по х
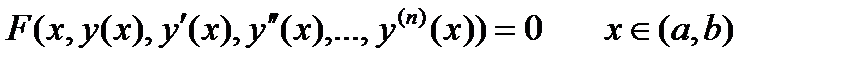
Для дифференциального уравнения 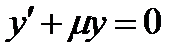 решением является функция
решением является функция 
Действительно,
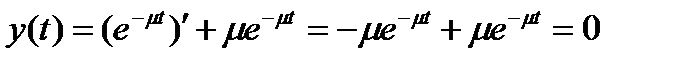
Рассмотрим еще одно уравнение
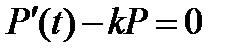
Решением является функция
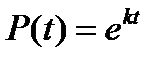
Действительно,

 2015-03-07
2015-03-07 1933
1933
