1.4.1. Полый тонкостенный цилиндр массой 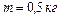 , катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену
, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 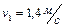 , после удара
, после удара 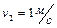 . Определить выделившееся при ударе количество теплоты. Ответ:
. Определить выделившееся при ударе количество теплоты. Ответ: 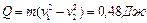 .
.
1.4.2. К ободу сплошного диска массой 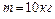 , насаженного на ось, приложена постоянная касательная сила
, насаженного на ось, приложена постоянная касательная сила 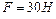 . Определить кинетическую энергию диска через время
. Определить кинетическую энергию диска через время 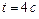 после начала действия силы. Ответ:
после начала действия силы. Ответ: 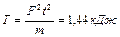 .
.
1.4.3. Шар радиусом 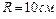 и массой
и массой 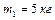 вращается вокруг оси симметрии согласно уравнению
вращается вокруг оси симметрии согласно уравнению 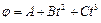 (
(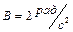 ,
, 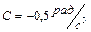 ). Определить момент сил, действующий на шар для момента времени
). Определить момент сил, действующий на шар для момента времени 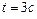 . Ответ:
. Ответ: 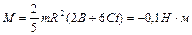 .
.
1.4.4. Вентилятор вращается с частотой 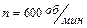 . После выключения он начал вращаться равнозамедленно и, сделав
. После выключения он начал вращаться равнозамедленно и, сделав 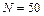 оборотов, остановился. Работа сил торможения равна
оборотов, остановился. Работа сил торможения равна 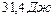 . Определить: 1)момент сил торможения; 2)момент инерции вентилятора. Ответ:
. Определить: 1)момент сил торможения; 2)момент инерции вентилятора. Ответ: 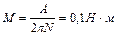 ,
, 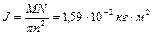 .
.
1.4.5. Сплошной однородный диск скатывается без скольжения с наклонной плоскости с углом при основании 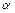 . Определить линейное ускорение центра диска. Ответ:
. Определить линейное ускорение центра диска. Ответ: 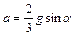 .
.
1.4.6. К ободу однородного сплошного диска радиусом 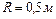 приложена постоянная касательная сила
приложена постоянная касательная сила 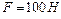 . При вращении диска на него действует момент сил трения
. При вращении диска на него действует момент сил трения 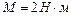 . Определить массу
. Определить массу 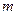 диска, если известно, что его угловое ускорение
диска, если известно, что его угловое ускорение 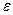 постоянно и равно
постоянно и равно 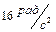 . Ответ:
. Ответ: 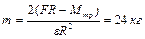 .
.
1.4.7. Маховик в виде сплошного диска, момент инерции которого 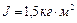 , вращаясь при торможении равнозамедленно, за время
, вращаясь при торможении равнозамедленно, за время 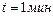 уменьшил частоту своего вращения с
уменьшил частоту своего вращения с 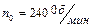 до
до 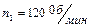 . Определить: 1)угловое ускорение
. Определить: 1)угловое ускорение 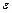 маховика; 2)момент силы торможения; 3)работу торможения. Ответ:
маховика; 2)момент силы торможения; 3)работу торможения. Ответ: 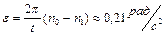 ,
, 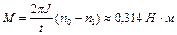 ,
, 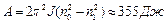 .
.
1.4.8. Колесо радиусом 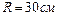 и массой
и массой 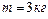 скатывается без трения по наклонной плоскости длиной
скатывается без трения по наклонной плоскости длиной 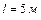 и углом при основании
и углом при основании 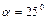 . Определить момент инерции колеса, если его скорость после скатывания составила
. Определить момент инерции колеса, если его скорость после скатывания составила 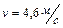 . Ответ:
. Ответ: 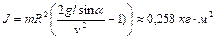 .
.
1.4.9. С наклонной плоскости с углом при основании 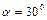 скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на
скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 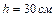 . Ответ:
. Ответ: 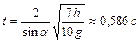 .
.
1.4.10. Полый тонкостенный цилиндр катится вдоль горизонтального участка дороги со скоростью 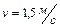 . Определить путь, который он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути. Ответ:
. Определить путь, который он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути. Ответ: 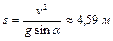 .
.
1.4.11. На однородный сплошной цилиндрический вал радиусом 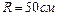 намотана легкая нить, к концу которой прикреплен груз массой
намотана легкая нить, к концу которой прикреплен груз массой 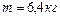 . Груз, разматывая нить, опускается с ускорением
. Груз, разматывая нить, опускается с ускорением 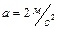 . Определить момент инерции
. Определить момент инерции 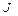 вала и массу
вала и массу 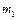 вала. Ответ:
вала. Ответ: 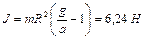 ,
, 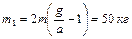 .
.
1.4.12. На однородный сплошной цилиндрический вал радиусом 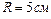 и массой
и массой 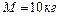 намотана легкая нить, к концу которой прикреплен груз массой
намотана легкая нить, к концу которой прикреплен груз массой 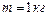 . Определить: 1)силу натяжения нити; 2)угловую скорость вала через
. Определить: 1)силу натяжения нити; 2)угловую скорость вала через 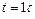 после начала движения; 3)тангенциальное и нормальное ускорения точек, находящихся на поверхности вала. Ответ:
после начала движения; 3)тангенциальное и нормальное ускорения точек, находящихся на поверхности вала. Ответ: 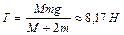 ,
, 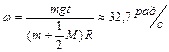 ,
, 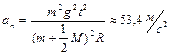 ,
, 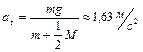 .
.
1.4.13. На однородный сплошной цилиндрический вал радиусом 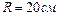 , момент инерции которого
, момент инерции которого 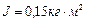 , намотана легкая нить, к концу которой прикреплен груз массой
, намотана легкая нить, к концу которой прикреплен груз массой 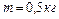 . До начала вращения барабана высота
. До начала вращения барабана высота 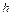 груза над полом составляла 2,3 м. Определить: 1)время опускания груза до пола; 2)силу натяжения нити; 3)кинетическую энергию груза в момент удара о пол. Ответ:
груза над полом составляла 2,3 м. Определить: 1)время опускания груза до пола; 2)силу натяжения нити; 3)кинетическую энергию груза в момент удара о пол. Ответ: 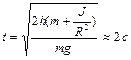 ,
, 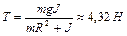 ,
, 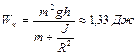 .
.
1.4.14. Через блок в виде однородного сплошного цилиндра массой 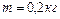 перекинута невесомая нить, к концам которой прикреплены тела массами
перекинута невесомая нить, к концам которой прикреплены тела массами 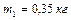 и
и 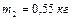 . Пренебрегая трением в оси блока, определить: 1)ускорение грузов; 2)отношение сил натяжения нити по разные стороны от блока. Ответ:
. Пренебрегая трением в оси блока, определить: 1)ускорение грузов; 2)отношение сил натяжения нити по разные стороны от блока. Ответ: 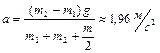 ,
, 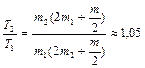 .
.
1.4.15. Тонкая однородная палочка длины 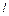 и массы
и массы 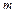 лежит симметрично на двух опорах, расстояние между которыми
лежит симметрично на двух опорах, расстояние между которыми 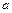 . Одну из опор быстро убирают. Какова сразу после этого сила реакции оставшейся опоры? Ответ:
. Одну из опор быстро убирают. Какова сразу после этого сила реакции оставшейся опоры? Ответ: 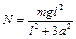 .
.
1.4.16. Для демонстрации законов сохранения применяется маятник Максвелла, представляющий собой массивный диск радиусом 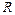 и массой
и массой 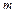 , туго насаженный на ось радиусом
, туго насаженный на ось радиусом 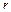 , которая подвешивается в горизонтальном положении на двух предварительно намотанных на нее нитях. Когда маятник отпускают, он совершает возвратно-поступательное движение в вертикальной плоскости при одновременном вращении диска вокруг оси. Не учитывая трения и пренебрегая моментом инерции оси определить: 1)ускорение поступательного движения; 2)силу натяжения нити. Ответ:
, которая подвешивается в горизонтальном положении на двух предварительно намотанных на нее нитях. Когда маятник отпускают, он совершает возвратно-поступательное движение в вертикальной плоскости при одновременном вращении диска вокруг оси. Не учитывая трения и пренебрегая моментом инерции оси определить: 1)ускорение поступательного движения; 2)силу натяжения нити. Ответ: 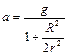 ,
, 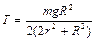 .
.
1.4.17. Однородный шар радиусом 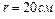 скатывается без скольжения с вершины сферы радиусом
скатывается без скольжения с вершины сферы радиусом 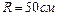 . Определить угловую скорость шара после отрыва от сферы. Ответ:
. Определить угловую скорость шара после отрыва от сферы. Ответ: 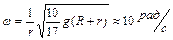 .
.
1.4.18. Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением 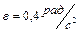 . Определить кинетическую энергию маховика через время
. Определить кинетическую энергию маховика через время 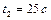 после начала движения, если через
после начала движения, если через 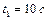 после начала движения момент импульса маховика составлял
после начала движения момент импульса маховика составлял 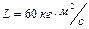 . Ответ:
. Ответ: 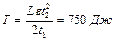 .
.
1.4.19. Горизонтальная платформа массой 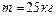 и радиусом
и радиусом 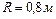 вращается с угловой скоростью
вращается с угловой скоростью 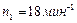 . В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от
. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 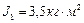 до
до 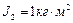 . Ответ:
. Ответ: 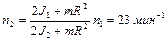 .
.
1.4.20. Человек, стоящий на скамье Жуковского, держит в руках стержень длиной 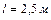 и массой
и массой 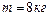 , расположенный вертикально вдоль оси вращения скамьи. Эта система (скамья и человек) обладает моментом инерции
, расположенный вертикально вдоль оси вращения скамьи. Эта система (скамья и человек) обладает моментом инерции 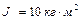 и вращается с частотой
и вращается с частотой 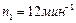 . Определить частоту
. Определить частоту 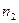 вращения системы, если стержень повернуть в горизонтальное положение. Ответ:
вращения системы, если стержень повернуть в горизонтальное положение. Ответ: 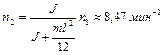 .
.
1.4.21. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы. Ответ: 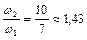 .
.
1.4.22. Человек массой 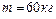 , стоящий на краю горизонтальной платформы радиусом
, стоящий на краю горизонтальной платформы радиусом 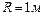 и массой
и массой 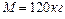 , вращающейся по инерции вокруг неподвижной вертикальной оси с частотой
, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 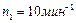 , переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру. Ответ:
, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру. Ответ: 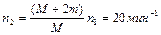 .
.
1.4.23. Однородный стержень длиной 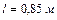 может свободно поворачиваться вокруг горизонтальной оси, проходящей через один из его концов. Стержень находится в положении устойчивого равновесия. Какую наименьшую скорость
может свободно поворачиваться вокруг горизонтальной оси, проходящей через один из его концов. Стержень находится в положении устойчивого равновесия. Какую наименьшую скорость 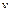 надо сообщить свободному концу, чтобы стержень сделал полный оборот вокруг своей оси? Ответ:
надо сообщить свободному концу, чтобы стержень сделал полный оборот вокруг своей оси? Ответ: 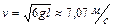 .
.
1.4.24. Бревно высоты  и массы
и массы 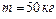 начинает падать из вертикального положения на землю. Определить скорость верхнего конца и момент импульса бревна в момент падения на землю. Ответ:
начинает падать из вертикального положения на землю. Определить скорость верхнего конца и момент импульса бревна в момент падения на землю. Ответ: 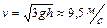 ,
, 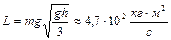 .
.
1.4.25. Карандаш длиной 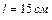 , поставленный вертикально, начинает падать на стол. Какую угловую скорость
, поставленный вертикально, начинает падать на стол. Какую угловую скорость 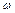 и линейную скорость
и линейную скорость 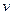 будут иметь в конце падения середина и верхний конец карандаша? Ответ:
будут иметь в конце падения середина и верхний конец карандаша? Ответ: 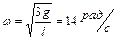 ,
, 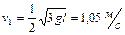 ,
, 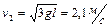 .
.
1.4.26. Однородный стержень длиной 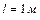 подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол
подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол 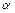 надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость
надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость 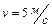 ?
? 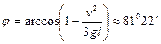 .
.
1.4.27. На горизонтальную ось насажены маховик и легкий шкив радиусом 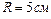 . На шкив намотан шнур, к которому привязан груз массой
. На шкив намотан шнур, к которому привязан груз массой 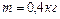 . Опускаясь равноускоренно, груз прошел путь
. Опускаясь равноускоренно, груз прошел путь 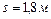 за время
за время 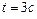 . Определить момент инерции маховика. Массу шкива считать пренебрежимо малой. Ответ:
. Определить момент инерции маховика. Массу шкива считать пренебрежимо малой. Ответ: 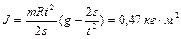 .
.
1.4.28. Шарик массой 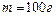 , привязанный к концу нити длиной
, привязанный к концу нити длиной 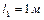 , вращается, опираясь на горизонтальную плоскость с частотой
, вращается, опираясь на горизонтальную плоскость с частотой 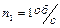 . Нить укорачивается, приближая шарик к оси вращения до расстояния
. Нить укорачивается, приближая шарик к оси вращения до расстояния 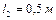 . С какой частотой
. С какой частотой 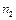 будет при этом вращаться шарик? Какую работу совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. Ответ:
будет при этом вращаться шарик? Какую работу совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. Ответ: 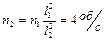 ,
, 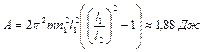 .
.
1.4.29. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой – вдоль вертикали вниз. Определить коэффициент трения между поверхностями груза и стола, если массы каждого груза и блока одинаковы и грузы движутся с ускорением 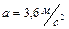 . Проскальзыванием нити по блоку и трением в блоке пренебречь. Блок считать однородным диском. Ответ:
. Проскальзыванием нити по блоку и трением в блоке пренебречь. Блок считать однородным диском. Ответ: 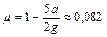 .
.
1.4.30. Однородный стержень длиной 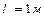 может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой
может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой 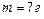 , летящая перпендикулярно стержню и его оси. Определить массу стержня, если в результате попадания пули он отклонился от вертикали на угол
, летящая перпендикулярно стержню и его оси. Определить массу стержня, если в результате попадания пули он отклонился от вертикали на угол 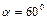 . Скорость пули равна
. Скорость пули равна 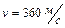 . Ответ:
. Ответ: 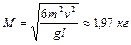 .
.
 2015-05-13
2015-05-13 3190
3190








