Уравнение для поправки давления

При получении (6.10) для поправки скорости было решено отбросить член Sa_nbu’_nb. Объясним теперь причину этого отбрасывания и покажем, что оно не приносит большого вреда.

Если бы такие члены, как a_nbu’_nb, не были отброшены, то их надо было бы выразить через скорректированные значения давления и скорости в соседних для u_nb узлах. Эти значения, в свою очередь, зависят от соответствующих значений в близлежащих соседних узлах и т.д. Т.е. формула для поправки скорости будет содержать скорректированное давление во всех узловых точках расчетной области и решение результирующего уравнения для поправки давления будет трудоемким. В сущности, мы будем приближаться к непосредственному решению всей системы уравнений количества движения и неразрывности, однако выбранный путь будет достаточно сложным. Отбрасывание члена a_nbu’_nb позволяет получить уравнение для p' в той же форме, что и основное уравнение для Ф, и применить последовательную процедуру решения для одной переменной на одном шаге по времени.

Слово «полунеявная» в названии SIMPLE использовалось для того, чтобы подчеркнуть отбрасывание члена Sa_nbu’_nb. Этот член характеризует непрямое или неявное влияние поправки давления на скорость; поправки давления в близлежащих точках могут изменять соседние значения скоростей и таким образом вызывать коррекцию скорости в рассматриваемой точке. Это влияние не учитывается и, следовательно, работаем со схемой которая является только частично, а не полностью неявной.

Отбрасывание любого члена будет, конечно, нежелательным, если это означает, что конечное решение не будет истинным решением дискретных аналогов уравнений количества движения и неразрывности. Однако оказывается, что сходящееся решение, которое получается с помощью SIMPLE, не содержит какой-либо ошибки, являющейся результатом отбрасывания Sa_nbu’_nb. В сходящемся решении достигаются такие поля давления, при которых соответствующие поля u^*, v^*, w^* удовлетворяют уравнению неразрывности. Детали построения уравнения для p' в этом случае не влияют на корректность сходящегося решения.

Полезно обратить внимание на действия в процессе последней итерации, после которой можно считать, что достигнута сходимость. В результате всех предыдущих итерации получаем некоторое поле давления. Использовав его как p ^*, решим уравнение количества движения, чтобы получить u^*, v^*, w^*. Из этого поля скорости рассчитаем массовый источник b для уравнения поправки давления. Поскольку речь идет о последней итерации, то значение b будет приближаться к нулю для всех КО. Следовательно, p'=0 для всех узловых точек - приемлемое решение уравнения (6.15) и значения u^*, v^*, w^* и p ^*будут сами по себе точными значениями давления и скоростей.

Таким образом, то, что массовый источник b является нулевым везде, есть достаточное доказательство того, что получено точное поле давления и текущее решение уравнения p' не нуждается в проведении последней итерации. Очевидно, сходящееся решение в этом случае не зависит от любых аппроксимаций, сделанных при получении уравнения для p'.

Т.е. массовый источник b служит полезным указателем сходимости решения уравнений, описывающих течение жидкости. Итерации должны повторяться до тех пор, пока b повсюду не станет достаточно малым.

Из этих соображений уравнение для поправки давления можно рассматривать просто как промежуточный алгоритм, который дает точное поле давления, но не оказывает непосредственного влияния на окончательное решение. До тех пор, пока мы не получим сходящееся решение, все возможные формулировки уравнения для p' дают одно и то же окончательное решение. Скорость сходимости процедуры, однако, зависит от конкретного вида записи уравнения для p'. Если будет опущено большое число членов, то результатом этого может быть расходимость.

Уравнение для поправки давления также может приводить к расходимости, если не используется некоторая нижняя релаксация. В большинстве случаев с успехом используется следующий способ: применяется нижняя релаксация для u^*, v^* и w^* (с соответствующими предыдущей итерации значениями u, v, w) при решении уравнения движения; в дальнейшем к p ^* добавляется только часть p'. Другими словами, вместо уравнений (6.6) и (6.7) применяется соответственно

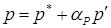(6.16)

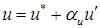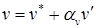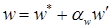, , . (6.17)

Необходимо отметить, что оптимальные значения коэффициентов релаксации обычно зависят от самой задачи. Хотя опыт предыдущих расчетов является полезным, новые задачи иногда требуют других релаксационных процедур.

В течение каждой итерации скорости корректируют с использованием формул для поправки скорости. Результирующие поля скорости точно удовлетворяют дискретному аналогу уравнения неразрывности независимо от того, что подлежащие коррекции давления являются только приближенными. Итак, в процессе расчетов сходимость достигается через ряд полей скорости, удовлетворяющих уравнению неразрывности. Эта особенность алгоритма SIMPLE имеет много преимуществ. Поле скорости, удовлетворяющее уравнению неразрывности, является более разумным, чем поле скоростей u^*, v^* и w^*. Использование нижней релаксации в отношении этих скоростей помогает поддерживать в разумных пределах значения скоростей u^*, v^* и w^* и массовые источники b малыми. К тому же решение других уравнений для Ф на каждой итерации может быть основано на поле течения, которое удовлетворяет балансу массы.

При получении уравнения для p' предполагалось, что плотность известна; влияние давления на плотность не учитывалось. Это можно рассматривать как дополнительное приближение в уравнении для p' и можно обосновать аналогичным образом. Суть любого итерационного метода состоит в том, что в уравнении уделяется внимание нескольким существенным воздействиям, а многие другие величины рассматриваются как условно известные, но рассчитываемые для следующей итерации.

Плотность рассчитывается из соответствующего уравнения состояния. Оно может включать зависимость от температуры, концентрации и даже от давления. До тех пор пока не будет получено сходящееся решение, приближенный вариант уравнения для p' является достаточным. Однако для сильно сжимаемых (особенно сверхзвуковых) потоков зависимость плотности от давления является настолько существенной, что появляется большая вероятность получить расходящееся решение. Можно ввести

.

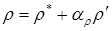Можно заметить, что уравнение для p' подобно дискретному аналогу уравнения теплопроводности. В формуле для поправки скорости коррекцию скорости u_e’, можно рассматривать, аналогично тепловому потоку, вызванному разностью температур (p_P’-p_E’).

Тип уравнения для p', подобного уравнению теплопроводности, означает, что одностороннее поведение проявляется по любой пространственной координате. Хорошо известно, что влияние давления является двухсторонним или эллиптическим. Одно стороннее поведение при течении в пограничных слоях достигается при введении дополнительного допущения о поле давлении, на пример в пограничных слоях изменением давления, нормального к стенке, пренебрегается ().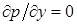

Сверхзвуковые потоки проявляют одностороннее поведение в том, что давление вниз по потоку не изменяет условий вверх по потоку. При расчетах сверхзвуковых потоков будем использовать уравнение для p' в особой «сжимаемой» форме

.

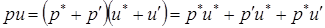Коэффициенты в этом уравнении подобны тем, которые имеют место в задачах конвекции и диффузии и, значит, делают применимым одностороннее поведение при соответствующих числах Маха.