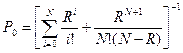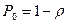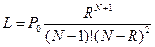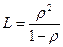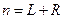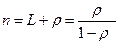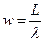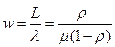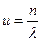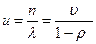Рассмотрим систему массового обслуживания (СМО), на вход которой поступает простейший поток заявок интенсивности 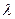 . Система имеет n каналов обслуживания. Заявка, пришедшая в систему и заставшая свободным хотя бы один канал, немедленно принимается на обслуживание и проходит его за случайное, распределенное по показательному закону, время со средним значением
. Система имеет n каналов обслуживания. Заявка, пришедшая в систему и заставшая свободным хотя бы один канал, немедленно принимается на обслуживание и проходит его за случайное, распределенное по показательному закону, время со средним значением 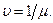 Очередь не ограничена, дисциплина выбора – FIFO.
Очередь не ограничена, дисциплина выбора – FIFO.
Обозначим через
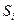
состояние СМО, в котором на обслуживании находится ровно i заявок, через
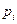
- вероятность состояния
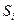
. Тогда смена состояний образует однородную неприводимую марковскую цепь, а вероятности
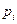
могут быть найдены из уравнений (1.1). Решая эти уравнения, получим:
Условие существования стационарного режима в данной СМО следующее: R < N, где R - среднее число занятых каналов.
Основные характеристики эффективности приведены в таблице 2.1.
Таблица 2.1.
| М/М/N/∞
(N каналов обслуживания)
| М/М/1/∞
(1 канал обслуживания)
|
| 1) R – среднее число занятых каналов
|
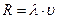
| 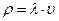
|
| 2) Р0 – вероятность простоя
|
|
|
| 3) L- среднее число заявок в очереди
|
|
|
| 4) n – среднее число заявок в системе
|
|
|
| 5) w - среднее время пребывания заявки в очереди
|
|
|
| 6) u – среднее время пребывания заявки в системе
|
|
|
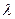 . Система имеет n каналов обслуживания. Заявка, пришедшая в систему и заставшая свободным хотя бы один канал, немедленно принимается на обслуживание и проходит его за случайное, распределенное по показательному закону, время со средним значением
. Система имеет n каналов обслуживания. Заявка, пришедшая в систему и заставшая свободным хотя бы один канал, немедленно принимается на обслуживание и проходит его за случайное, распределенное по показательному закону, время со средним значением 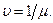 Очередь не ограничена, дисциплина выбора – FIFO.
Очередь не ограничена, дисциплина выбора – FIFO.
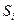 состояние СМО, в котором на обслуживании находится ровно i заявок, через
состояние СМО, в котором на обслуживании находится ровно i заявок, через 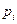 - вероятность состояния
- вероятность состояния 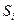 . Тогда смена состояний образует однородную неприводимую марковскую цепь, а вероятности
. Тогда смена состояний образует однородную неприводимую марковскую цепь, а вероятности 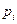 могут быть найдены из уравнений (1.1). Решая эти уравнения, получим:
могут быть найдены из уравнений (1.1). Решая эти уравнения, получим:
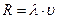
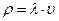
 2015-05-13
2015-05-13 369
369