2015-05-26
1293
На рисунке 3.45 приведена цепь с последовательным соединением r, L, C, по которой протекает ток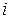 
, равный 
.
 |
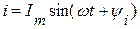Запишем второй закон Кирхгофа для мгновенных значений напряжений:
.
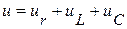Выражение второго закона Кирхгофа для действующих значений справедливо в векторной форме и для комплексов напряжений имеет вид:
.
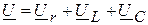Сформируем комплексные векторы тока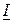 
и напряжени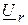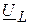й 
, 
и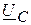 
.
1. Используя выражение мгновенного значения тока, сформируем комплекс действующего значения тока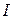 
(либо комплекса амплитуды 
):
.
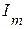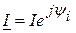
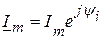2. Сформируем векторы падений напряжений на каждом элементе.
2.1. Падение напряжения на резистивном элементе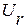 
связано с током 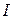законом Ома в виде 
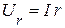, а их вектора совпадают по направлению. Тогда
.
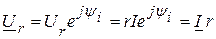2.2. Комплекс падения напряжения на индуктивном элементе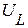 
, связан с током 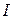законом Ома в виде 
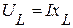, а вектор тока 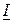отстает от вектора напряжения 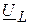на угол 900, следовательно
.
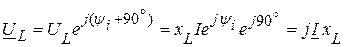2.3. Комплекс падения напряжения на емкостном элементе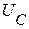 
, связан с током 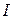законом Ома в виде 
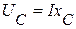, а вектор тока 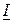опережает вектор напряжения 
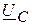на угол 900, следовательно
.
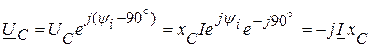3. Принимая во внимание вышеизложенное, второй закон Кирхгофа в комплексной форме будет иметь вид:
.
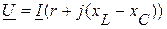Выражение в скобках называют комплексным сопротивлением:
,
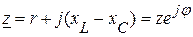где j – угол сдвига по фазе между током и напряжением на зажимах данной цепи.
Выражение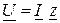 
называют законом Омав комплексной форме.
Из вышеуказанного следует, что при формировании комплексного сопротивления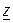 
, действительная часть представляет собой активное сопротивление 
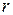, а мнимая часть – реактивное сопротивление 
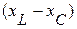. При этом сопротивления на индуктивности берутся с положительным знаком, а на емкости – с отрицательным.
Комплексное сопротивление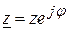 
, записанное в показательной форме, позволяет оценить полное сопротивление цепи 
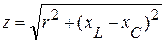и сдвиг по фазе 
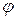между током 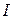и напряжением 
.
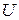По аналогии с цепями постоянного тока, можно записать законы Кирхгофа в комплексной форме:
I закон Кирхгофа: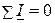 
II закон Кирхгофа: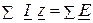 
.
Все методы расчета, которые ранее использовались для цепей постоянного тока, пригодны и для цепей синусоидального тока; но все расчеты должны выполняться в комплексной форме.
