Циркуляция и ротор векторного поля

Циркуляцией векторного поля, например, 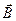вдоль какой-либо воображаемой замкнутой кривой L называется ска­лярная физическая величина, определяемая формулой:

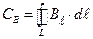(13.15)

Что характеризует циркуляция поля? Рассмотрим картину силовых линий полей на рис. 13.3. Во всех трех случаях источники отсутствуют. Но структура полей явно различна.

Поле на рис.13.3а имеет замкнутые силовые линии и при обходе контура L ка­сательная составляющая поля 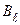сохраняет знак.

Рис.13.3. Примеры различных значений циркуляции.

Поэтому для поля на рис.13.3б обход контура L дает на двух сторонах квадрата нулевое значение интеграла (13.15),так как там 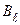= 0, а на двух других сторонах его численное значение одинаково, но имеет противоположный знак, в результате 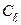=О. Поле на рис.13.3в, хотя и не имеет замкнутых линий, но обладает некоторой степенью "закрученности" своих силовых линий и в результате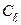 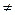0.

Гидродинамическая аналогия: в поле скоростей циркуляция определяется характером течения жидкости. Еcли жидкость течет с завихрениями, образует водовороты, воронки и т.п. то 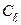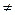0.

Ограниченность гидродинамической аналогии в применении к электромагнитного полям очевидна: в поле ничто реально не циркулирует и не образует "водоворотов". Вместе с тем, наглядный образ циркуляции, как степени закрученности силовых линий поля, весьма полезен.

13.4.1.Теорема о циркуляции вектора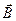

Метод определения полей систем движущихся зарядов или токов основан на введении математической характеристики векторных полей - циркуляции век­тора (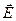 или ).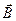

Элементарная циркуляция вектора 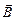вдоль элемента контура : .

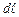циркуляция вектора 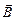вдоль контура L (рис. 13.4): .

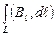циркуляция вектора 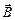вдоль замкнутого контура L: ,

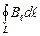где 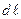- элемент данного контура ;

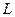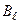- проекция вектор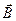а на 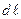(рис. 13.4).

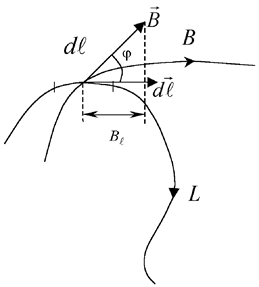
Рис. 13.4. К понятию циркуляции вектора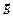

Выберем контур, совпадающий с силовой линией магнитного поля. Тогда вектор 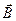совпадет по направлению с касательной компонентой 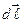к контуру .

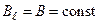Нетрудно показать, что если контур не охватывает ток, то цир­куляция вектора 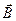равна нулю.

Теорема о циркуляции вектора 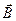(закон Ампера – закон полного тока):

Циркуляция вектора 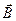вдоль любого замкнутого контура рав­на алгебраической сумме токов, пронизывающих площадку S, огра­ниченную контуром L, умноженной на магнитную постоянную 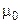(в системе СИ). (За положительное направление тока принимается направление, связанное с обходом контура по правилу правого винта):

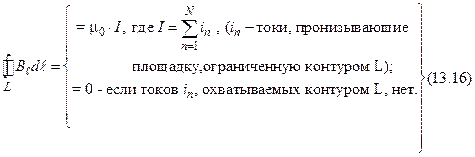
(в наиболее общем случае ).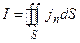

В дифференциальной форме теорема о циркуляции вектора 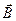выражается так:

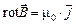. (13.17)

Здесь 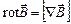– вихрь (ротор) магнитного поля,

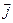– плотность тока.

Из теоремы о циркуляции в магнитостатике следует, что магнитное поле – вихревое и создается постоянными электрическими токами или движущимися зарядами. Направление закрученности силовых линий магнитного поля определяется направлением вектора 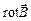(по правилу правого винта) (рис. 13.5).

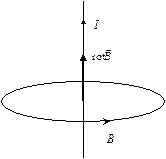
Рис.13.5. К понятию ротора вектора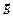

Теорема о циркуляции имеет следующий физический смысл:

I. силовые линии магнитного поля замкнуты; магнитное поле

носит вихревой характер (вихревое поле);

2. магнитное поле создается движущимися зарядами (токами);

3.теорема о циркуляции - метод расчета магнитных полей, созда­ваемых различными системами постоянных токов.

13.4.2.Циркуляция и ротор вектора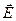

Для электростатического поля 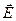циркуляция и ротор равны нулю:

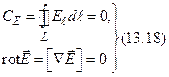
что подтверждает потенциальный характер этого поля (силовые линии электростатического поля не замкнуты – либо расходятся, либо сходятся).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Может ли поток вектора В через замкнутую поверхность быть отличным от нуля?

2. Чему равна циркуляция вектора напряженности электростатического поля вдоль замкнутого контура?

1. Какой знак имеет дивергенция вектора напряженности электростатического поля отрицательного заряда? положительного заряда?
2. В каком гипотетическом случае дивергенция вектора магнитной индукции может быть отлична от нуля?
3. Существует ли электрическое поле, ротор вектора напряженности которого отличен от нуля?