Методы формирования уравнений электрического равновесия цепи, основанные на непосредственном применении законов Кирхгофа, позволяют уменьшить число одновременно решаемых уравнений до b.
Первый закон Кирхгофа формулируется следующим образом: алгебраическая сумма токов ветвей, соединенных в узле, равна нулю
ΣIq = 0, (1)
где с положительным знаком учитываются токи, направленные от узла.
Второй закон Кирхгофа: алгебраическая сумма напряжений на ветвях любого контура равна нулю
ΣUk = 0, (2)
или в любом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на сопротивлениях, входящих в этот контур
ΣRkIk = Ek, (3)
В этом уравнении положительные знаки принимаются для токов и э.д.с., положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
При составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выполнить эквивалентные преобразования, выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить q – 1 уравнение на основании первого закона Кирхгофа и, наконец, составить b – (q – 1) уравнения для контуров на основании второго закона Кирхгофа.
Получить независимые уравнения по первому и второму законам Кирхгофа, т.е. выбрать независимую систему сечений и контуров, можно при помощи дерева графа схемы, содержащего все узлы графа, но ни одного контура, и ветвей связи, дополняющих дерево до исходного графа.
Если граф содержит b ветвей и q узлов, то число ветвей дерева
d = q- 1, а число ветвей связи k = b - (q-1). Для дерева образуется d главных сечений, каждое из которых состоит из ветвей связи и одной ветви дерева, и k главных контуров, каждый из которых состоит из ветвей дерева и только одной ветви связи. Уравнения, составленные по законам Кирхгофа для главных сечений и главных контуров, линейно независимы.
Следует помнить, что на графе электрической цепи ветви, содержащие идеальные источники тока, не показываются.
Например, для сложной электрической цепи (рис. 1) её граф представлен на рис. 2. Он содержит пять ветвей, следовательно необходимо записать пять уравнений: из них два на основании первого закона Кирхгофа (q – 1 = 3 – 1 = 2), остальные – на основании второго закона Кирхгофа.
Исходная система уравнений запишется в виде:
Узел 1 – I1 – I2 – I3 – J3 = 0
Узел 2 I3 + J3 + I5 – I4 – J4 = 0
Контур 1-2 R1I1 – R2I2 = E1 + E2
Контур 1-3-5 R1I1 – R3I3 + R5I5 = E1 – E3 + E5
Контур 4-5 R4I4 + R5I5 = E5
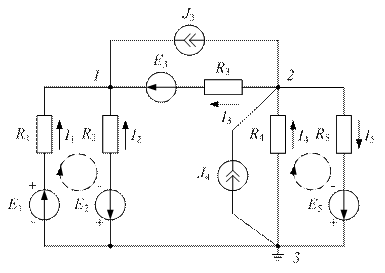
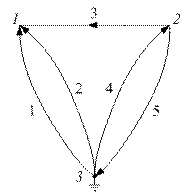
Рис. 1 Рис. 2
Если Е1 = 3 В, J3 = 1 A, R1 = 4 Ом,
Е2 =Е5 = 2 В, J4 = 0,5 A, R2 = 6 Ом,
Е3 = 1 В, R3 = 2 Ом,
R4 = 8 Ом,
R5 = 10 Ом,
то
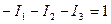
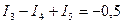
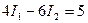 (4)
(4)
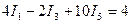
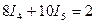
или
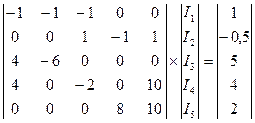 ,
,
А*х = В, откуда х = А-1*В.
Решение этой системы уравнений в MATLAB и MathCad приведено ниже.
1) Using Toolbox Path Cache. Type "help toolbox_path_cache" for more info. To get started, select "MATLAB Help" from the Help menu.
>> A=[-1 -1 -1 0 0; 0 0 1 -1 1; 4 -6 0 0 0; 4 0 -2 0 10; 0 0 0 8 10]
A =
-1 -1 -1 0 0
0 0 1 -1 1
4 -6 0 0 0
4 0 -2 0 10
0 0 0 8 10
>> B=[1; -0,5; 5; 4; 2]
B =
1.0000
-0.5000
5.0000
4.0000
2.0000
>> AI=inv(A)
AI =
-0.4372 -0.3015 0.0729 0.0678 0.0377
-0.2915 -0.2010 -0.1181 0.0452 -0.0251
-0.2714 0.5025 0.0452 -0.1131 0.0628
-0.1508 -0.2764 0.0251 -0.0628 0.0905
0.1206 0.2211 -0.0201 0.0503 0.0276
>> I=AI*B
I =
0.274
-0.651
-0.623
0.043
0.166
2)
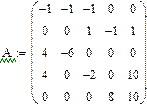 |
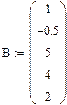 |
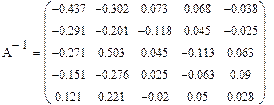 |
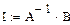 |
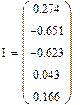 |
Схема замещения в программе multisim
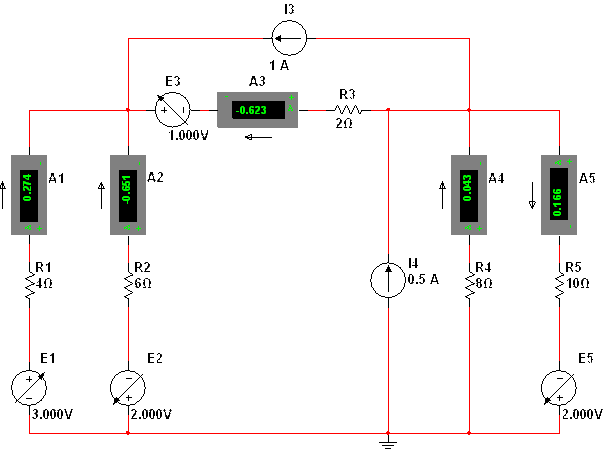
Рис. 3
 2015-05-26
2015-05-26 969
969








