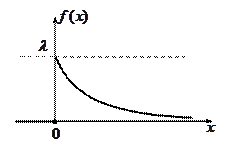 Говорят, что НСВ
Говорят, что НСВ 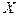 имеет показательный (экспоненциальный) закон распределения (
имеет показательный (экспоненциальный) закон распределения (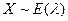 ), если
), если 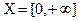 , а
, а 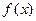 определяется, как:
определяется, как:
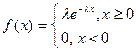 .
.
Проверим условие нормировки:
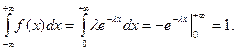 .
.
Найдем ФР:
-
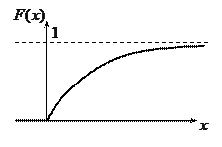
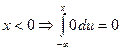 ;
; -
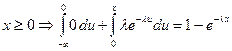 .
.
В точке 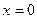 - происходит разрыв
- происходит разрыв 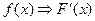 - не существует.
- не существует.
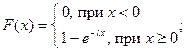
Рассчитаем МО и Д равномерной СВ:
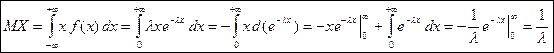
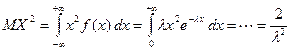
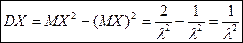
Нормальный (Гауссовский) ЗР, смысл его параметров.
Говорят, что НСВ 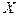 имеет нормальный (гауссовский) закон распределения с параметрами
имеет нормальный (гауссовский) закон распределения с параметрами 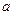 и
и 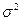 и обозначается
и обозначается 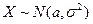 , если множество ее возможных значений
, если множество ее возможных значений 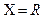 , а плотность вероятностей:
, а плотность вероятностей:
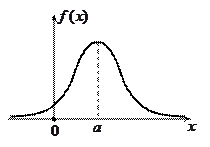
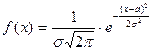 , где
, где 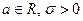 .
.
График плотности симметричен относительно прямой 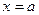 и принимает наибольшее значение в точке
и принимает наибольшее значение в точке 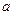 и
и 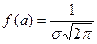 .
.
Проверим выполнение условия нормировки:
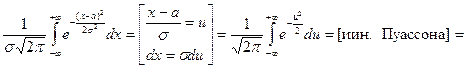
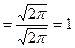 .
.
При 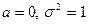 , то
, то 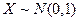 - стандартная нормальная СВ.
- стандартная нормальная СВ.
Его ФР: 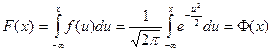 - функция Лапласа.
- функция Лапласа.
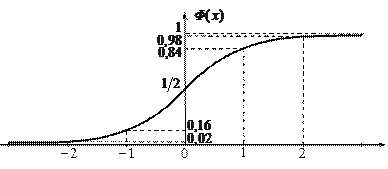
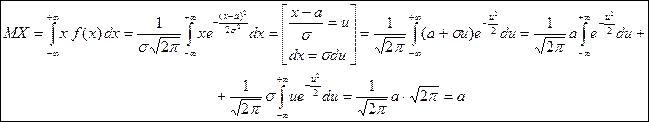
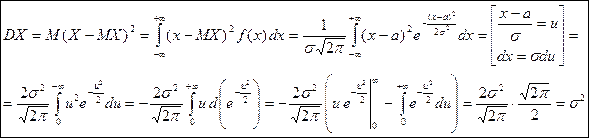
 2015-05-30
2015-05-30 677
677








