Исследовать функцию на монотонность и экстремум

№1. Исследовать функцию на монотонность и экстремум .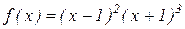

Решение.

1) D (f)= R

2)

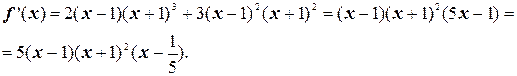
3) 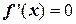при , , .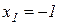

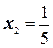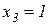–1, 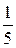, 1 – критические точки, так как внутренние точки области определения и .

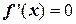4) Выясним знаки производной:

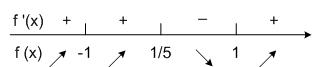
Функция y = f (x) возрастает на промежутках (–∞; 1/5]; [1;+∞).

Функция y = f (x) убывает на промежутке [1/5; 1].

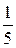– точка максимума, f (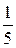) – максимум функции.

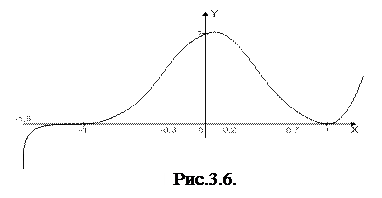
1 – точка минимума, f (1) – минимум функции (рис. 3.6.1).

 

№2. Исследовать функцию на выпуклость и вогнутость.

Найти точки перегиба: .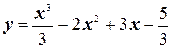

Решение.

1) D (f)= R

2) .

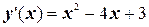3) .

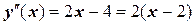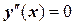при .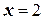

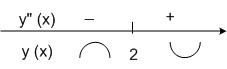
Функция y = f (x) выпуклая на промежутке (–∞; 2].

Функция y = f (x) вогнутая на промежутке [2; +∞).

(2;–1) – точка перегиба.

№ 3. Найти вертикальные асимптоты линии:

а) y =tg x;

б) .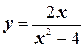

Решение.

а) Так как данная функция имеет разрыв в точках x = 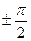, то , .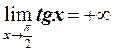

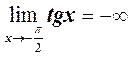Следовательно, 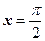, 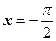– вертикальные асимптоты.

б) Функция 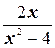имеет бесконечный предел при х ®2 и х ® -2.

 

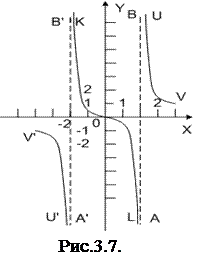Значит, прямые х = 2 и х = -2 (АВ и А′В′ на рис. 3.6.2) – асимптоты. Прямая АВ служит асимптотой для двух ветвей, UV и KL. Вдоль первой бесконечное удаление направлено вверх, вдоль второй – вниз (ибо 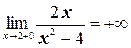и 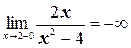. Аналогично для прямой А′В′.

Заметим, что прямая х=0 служит горизонтальной асимптотой (для ветвей UV и U′V′).

№ 4. Исследовать функцию 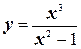и построить ее график.

Решение.

1. Находим область определения функции: (–¥; –1) È (–1; 1) È (1; ¥).

2. Точки пересечения с осью ОХ: у =0, тогда

,

х =0, => (0; 0) – точка пересечения с осью ОХ.

Точки пересечения с осью ОУ: х =0, тогда

,

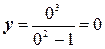у =0, => (0; 0) – точка пересечения с осью ОУ.

3. Область определения симметрична относительно нуля

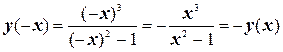
Таким образом, функция является нечетной.

4. Так как точки х = 1, х = –1 являются точками разрыва, то вычислим следующие пределы:

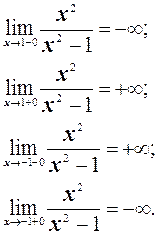
Значит х = 1, х = –1 – вертикальные асимптоты.

Теперь найдем наклонные асимптоты.

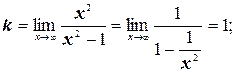
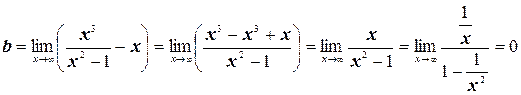
Итого, уравнение наклонной асимптоты – y = x.

5. Находим критические точки.

Найдем производную функции

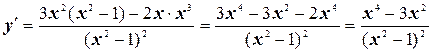
Критические точки: x = 0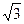; x = – ; x = 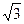; x = –1; x = 1.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

x < – 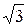, y ¢ > 0, функция возрастает

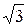– < x < –1, y ¢ < 0, функция убывает

–1 < x < 0, y ¢ < 0, функция убывает

0 < x < 1, y ¢ < 0, функция убывает

1 < x < 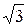, y ¢ < 0, функция убывает

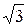< x, y ¢ > 0, функция возрастает

Видно, что точка х = – 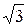является точкой максимума, а точка х = 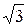является точкой минимума. Значения функции в этих точках равны соответственно: – 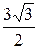и .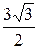

6. Найдем вторую производную функции

.

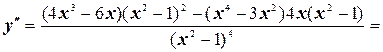
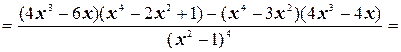
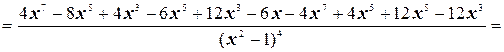
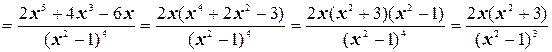Определим выпуклость и вогнутость кривой на промежутках.

x < –1, y¢¢ < 0, кривая выпуклая

–1 < x < 0, y¢¢ > 0, кривая вогнутая

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x, y¢¢ > 0, кривая вогнутая

–1, 0, 1 – точки перегиба.

7. Построим график функции:

.

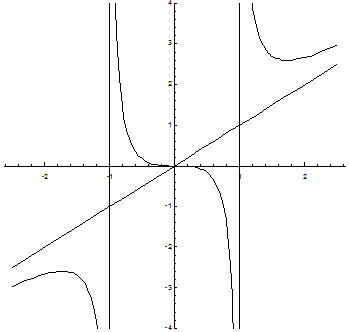
8. Область значения E (y)= R.

Варианты заданий

№ 3.1. Найти интервалы монотонности следующих функций:

 

1. ;

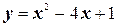2. ;

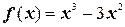3. ;

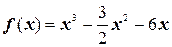4. 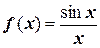на ;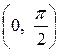

5. .

 

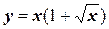№ 3.7.2. Исследовать на экстремум следующие функции:

 

1. ;

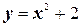2. ;

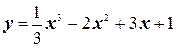3. ;

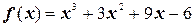4. ;

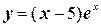5. .

 

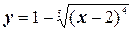№ 3.3. Исследовать на выпуклость и вогнутость следующие функции:

 

1. ;

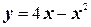2. ;

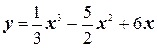3. ;

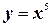4. ;

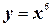5. .

 

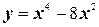№ 3.4. Найти наибольшее и наименьшее значения функции:

1. 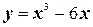на отрезке ;

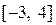2. 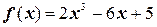на отрезке ;

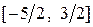3. 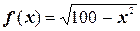на отрезке .

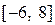№ 3.5. Исследовать функции и построить их графики:

1. y =3 x ⁵–5 x ³+2;

2. y= ;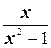

3. y= ;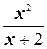

4. y= ;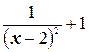

5.

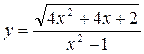
6.

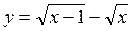
7.

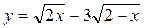
8.

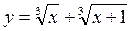
9.

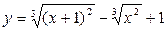
10.

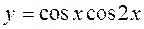
11.

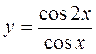
12.

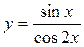
13. у = tg(x) – sin(x)

14. y = ctg(x) + cos(x)