Пусть кривая  является графиком непрерывной функции
является графиком непрерывной функции 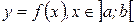 (рис. 8)
(рис. 8)
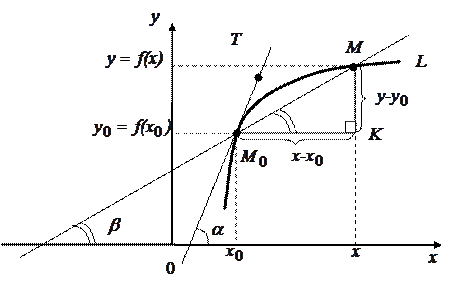
Рис. 8
На кривой  рассмотрим точки
рассмотрим точки 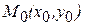 и
и 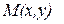 и проведем секущую
и проведем секущую 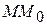 . Очевидно, если
. Очевидно, если 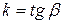 – это ее угловой коэффициент, то из
– это ее угловой коэффициент, то из 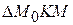 мы видим, что он равен:
мы видим, что он равен: 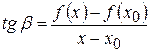 .
.
Пусть теперь 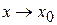 , то есть абсцисса точки
, то есть абсцисса точки 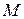 приближается к абсциссе точки
приближается к абсциссе точки 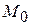 и, следовательно, точка
и, следовательно, точка 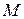 стремится к точке
стремится к точке 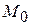 , оставаясь на кривой
, оставаясь на кривой 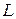 . При этих условиях секущая
. При этих условиях секущая 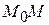 меняет свое положение, вращаясь вокруг точки
меняет свое положение, вращаясь вокруг точки 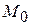 , то есть изменяется угол
, то есть изменяется угол 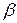 .
.
Если функция 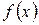 дифференцируема в точке
дифференцируема в точке 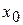 , то
, то 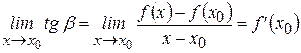 , и следовательно, существует прямая
, и следовательно, существует прямая 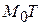 , являющаяся предельным положением секущей
, являющаяся предельным положением секущей 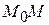 , при приближении точки
, при приближении точки 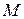 по кривой
по кривой 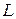 к точки
к точки 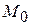 . Эта прямая, как известно, будет касательной к кривой
. Эта прямая, как известно, будет касательной к кривой 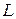 в точке
в точке 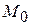 . Таким образом, если функция
. Таким образом, если функция 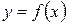 дифференцируема в точке
дифференцируема в точке 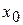 , то ее график имеет касательную в точке
, то ее график имеет касательную в точке 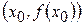 , угловой коэффициент которой равен
, угловой коэффициент которой равен 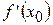 , (так как
, (так как 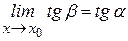 , то
, то 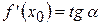 ).
).
Сказанное позволяет дать следующее геометрическое истолкование производной:
Производная функции 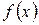 в точке
в точке 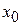 равна угловому коэффициенту касательной к графику функции в точке
равна угловому коэффициенту касательной к графику функции в точке 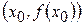 , то есть
, то есть 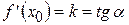 .
.
Примеры: 1. В какой точке касательная к кривой 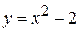
1) параллельна оси 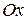 ;
;
2) образует с осью 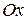 угол в 45o?
угол в 45o?
Решение:
1) Так как касательная параллельна оси 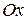 , то она образует с ней угол
, то она образует с ней угол 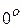 и ее угловой коэффициент
и ее угловой коэффициент 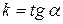 в точке касания равен нулю, так как
в точке касания равен нулю, так как 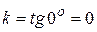 . Воспользуемся геометрическим смыслом производной
. Воспользуемся геометрическим смыслом производной 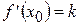 и составим уравнение:
и составим уравнение: 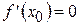 .
.
Найдем производную функции 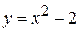 :
: 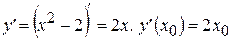 .
.
Тогда 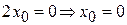 , откуда
, откуда 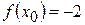 .
.
Итак, касательная к данной кривой параллельна оси 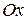 в точке (0;-1)
в точке (0;-1)
2) Так как касательная образует с осью 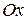 угол в 45о, то ее угловой коэффициент
угол в 45о, то ее угловой коэффициент 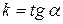 равен 1, так как
равен 1, так как 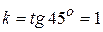 . Ранее мы нашли производную функции
. Ранее мы нашли производную функции 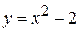 в любой ее точке:
в любой ее точке: 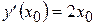 . Найдем значение аргумента, при котором эта производная равна 1, то есть решим уравнение
. Найдем значение аргумента, при котором эта производная равна 1, то есть решим уравнение 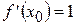 :
:
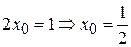 , откуда
, откуда 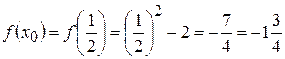 . Итак, касательная к данной кривой составляет с осью
. Итак, касательная к данной кривой составляет с осью 
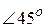 в точке
в точке 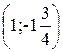 .
.
2. Найти угловой коэффициент касательной, приведенной к кривой 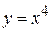 в точке
в точке 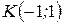 .
.
Решение:
Найдем производную функции 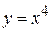 , получим
, получим 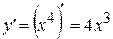 . По условию
. По условию 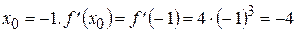
Итак, угловой коэффициент касательной кривой 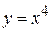 в точке
в точке 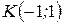 равен -4;
равен -4;
 2015-05-30
2015-05-30 1630
1630
