Производную от данной функции принято еще называть первой производной или производной первого порядка. Очевидно, что производная также является функцией, и если она дифференцируема, то от нее также можно взять производную.
Производную от производной первого порядка называют второй производной или производной второго порядка и обозначают  ,
, 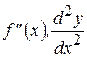 .
.
Пример: Найти вторую производную следующих функций:
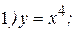
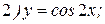
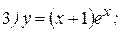
Решение:
1) Найдем первую производную:
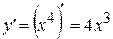 . Теперь найдем вторую производную
. Теперь найдем вторую производную
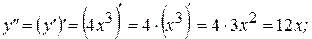
2) 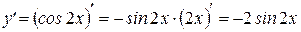 ;
;
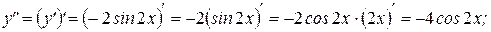
3) 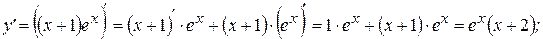
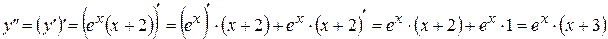 .
.
Далее рассмотрим механический (физический) смысл второй производной:
Пусть тело движется по закону 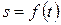 и его скорость в данный момент времени равна производной пути по времени, то есть
и его скорость в данный момент времени равна производной пути по времени, то есть 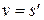 , тогда ускорение прямолинейного движения тела в данный момент времени равно второй производной пути по времени или первой производной скорости по времени, то есть
, тогда ускорение прямолинейного движения тела в данный момент времени равно второй производной пути по времени или первой производной скорости по времени, то есть 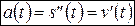 .
.
Примеры
1) Точка движется прямолинейно по закону 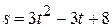 . Найти ускорение точки в момент
. Найти ускорение точки в момент 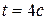 .
.
Решение: Найдем скорость данной точки. Для этого найдем производную от пути: 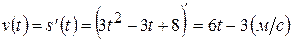 . Теперь найдем ускорение, для этого найдем вторую производную от пути:
. Теперь найдем ускорение, для этого найдем вторую производную от пути:
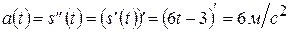 .
.
Величина ускорения оказалась постоянной для любого значения 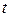 , значит движение точки по заданному закону происходит с постоянным ускорением, то есть
, значит движение точки по заданному закону происходит с постоянным ускорением, то есть 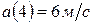 .
.
2) Закон движения тела определяется уравнением 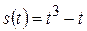 . Каково ускорение тела в момент, когда его скорость равна 11 м/с?
. Каково ускорение тела в момент, когда его скорость равна 11 м/с?
Решение: Найдем ускорение тела в любой момент времени, для этого найдем вторую производную от пути:
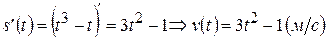
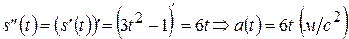
Далее решим уравнение 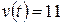 и найдем нужный нам момент времени:
и найдем нужный нам момент времени: 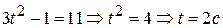 . Теперь найдем ускорение тела в момент
. Теперь найдем ускорение тела в момент 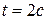 :
: 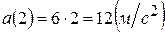 .
.
Упражнения
I Найти ускорение точки в указанные моменты времени 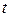 , если скорость точки, движущейся прямолинейно, определяется законом:
, если скорость точки, движущейся прямолинейно, определяется законом:
1) 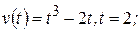
2) 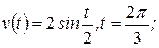
3) 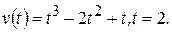
II Найти скорость и ускорение точки в указанные моменты времени 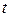 , движущейся прямолинейно по закону:
, движущейся прямолинейно по закону:
1) 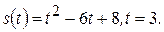
2) 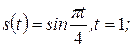
3) 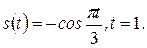
III Найти момент времени 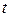 , в который ускорение точки, движущейся прямолинейно по закону
, в который ускорение точки, движущейся прямолинейно по закону 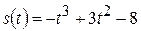 , равно нулю. Какова при этом скорость точки?
, равно нулю. Какова при этом скорость точки?
IV Тело массы m движется по закону 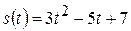 . Доказать, что сила, действующая на точку, постоянна.
. Доказать, что сила, действующая на точку, постоянна.
V Найти интервалы монотонности функций:
1) 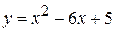 ; ; | 2) 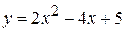 ; ; |
3) 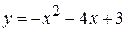 ; ; | 4) 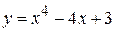 ; ; |
5) 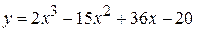 ; ; | 6) 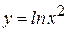 ; ; |
7) 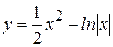 ; ; | 8) 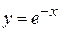 ; ; |
 2015-05-30
2015-05-30 11519
11519
