1 Вначале найдем производную функции 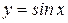 . Для этого воспользуемся определением производной:
. Для этого воспользуемся определением производной:
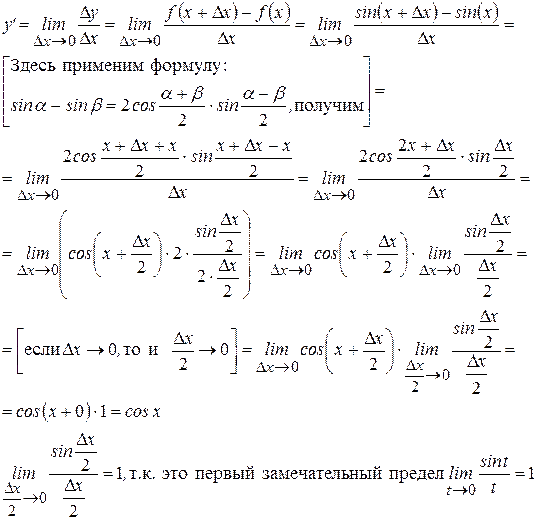
то есть
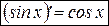 . (6)
. (6)
С помощью правила дифференцирования сложной функции получим формулу для нахождения производной сложной функции 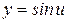 , где
, где 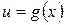 :
:
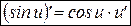 . (6’)
. (6’)
Примеры: Найти производные следующих функций:
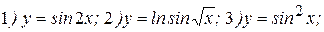
Решение:
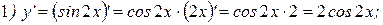
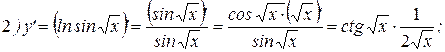
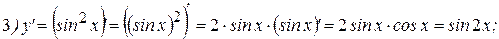
2Теперь найдем производную функции 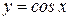 . Для этого представим функцию
. Для этого представим функцию 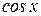 через функцию
через функцию 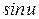 , с помощью формул приведения получим:
, с помощью формул приведения получим:
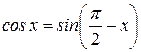 . Следовательно,
. Следовательно,
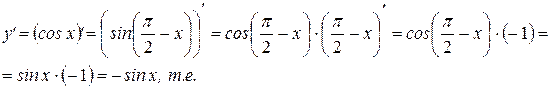
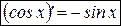 . (7)
. (7)
Для вывода формулы (7) можно также использовать определение производной. Чтобы найти производную сложной функции 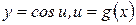 применим правило дифференцирования сложной функции и получим:
применим правило дифференцирования сложной функции и получим:
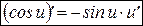 . (7’)
. (7’)
Примеры: Найти производные следующих функций:
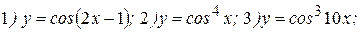
Решение:
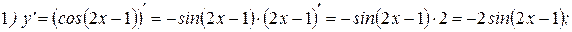
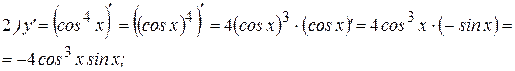
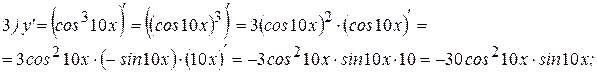
3Далее найдем производную функции 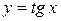 . Для этого воспользуемся определением тангенса и правилом дифференцирования дроби:
. Для этого воспользуемся определением тангенса и правилом дифференцирования дроби:
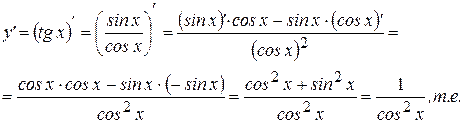
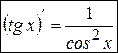 . (8)
. (8)
Для нахождения производной сложной функции 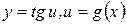 , применим правило дифференцирования сложной функции и получим, что:
, применим правило дифференцирования сложной функции и получим, что:
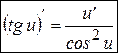 . (8’)
. (8’)
4 Аналогичным образом найдем производную функций 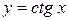 и
и 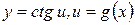 :
:
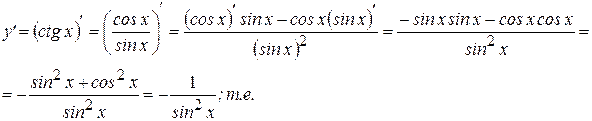
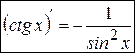 . (9)
. (9)
Для функции 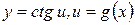 имеем:
имеем:
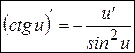 . (9’)
. (9’)
Примеры: Найти производные следующих функций:
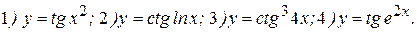
Решение:
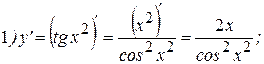
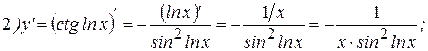
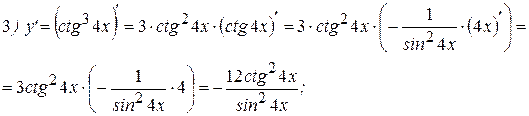
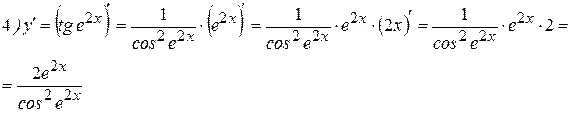
 2015-05-30
2015-05-30 2103
2103
