1Найдем производную функции 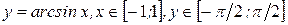 , согласно определению арксинуса имеем
, согласно определению арксинуса имеем 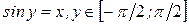 . Продифференцируем обе части последнего равенства по аргументу x, учитывая, что
. Продифференцируем обе части последнего равенства по аргументу x, учитывая, что 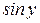 – сложная функция, так как y зависит от x. Получим:
– сложная функция, так как y зависит от x. Получим:
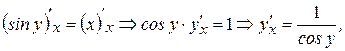 так как
так как 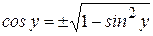 , а по условию
, а по условию 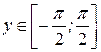 , поэтому выбираем положительное значение, то
, поэтому выбираем положительное значение, то 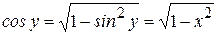 (так как
(так как 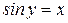 , по условию)
, по условию) 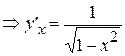 , то есть
, то есть
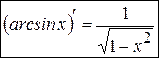 . (10)
. (10)
Для функции 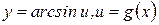 , используя правило дифференцирования сложной функции и получим, что:
, используя правило дифференцирования сложной функции и получим, что:
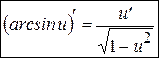 . (10’)
. (10’)
Примеры: Найти производные следующих функций:
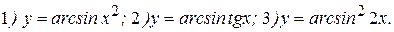
Решение:
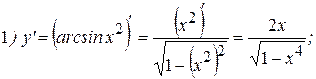
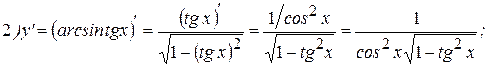
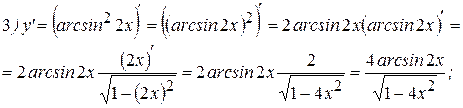
2Найдем производную функции 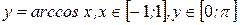 . Из определения арккосинуса имеем
. Из определения арккосинуса имеем 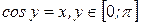 . Продифференцируем обе части последнего равенства по аргументу
. Продифференцируем обе части последнего равенства по аргументу 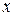 , учитывая, что
, учитывая, что 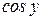 – сложная функция, так как y зависит от
– сложная функция, так как y зависит от 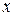 .
.
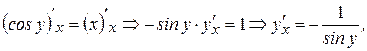 так как
так как 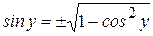 , и по условию
, и по условию 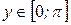 , поэтому выбираем положительное значение
, поэтому выбираем положительное значение 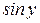 ,и подставляя вместо
,и подставляя вместо 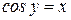 получим:
получим: 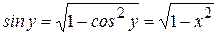
 , то есть
, то есть
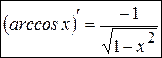 . (11)
. (11)
Для функции 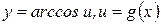 , используя правило дифференцирования сложной функции и получим, что
, используя правило дифференцирования сложной функции и получим, что
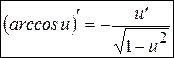 . (11’)
. (11’)
Примеры: Найти производные следующих функций:
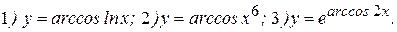
Решение:
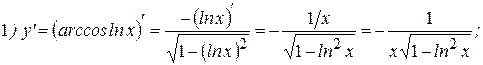
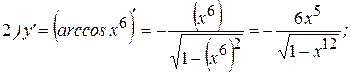
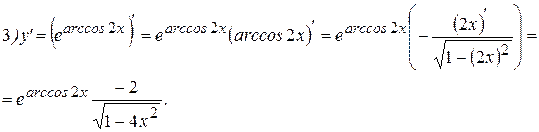
3 Далее найдем производную функции 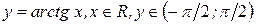 . Из определения арктангенса имеем
. Из определения арктангенса имеем 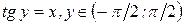 . Продифференцируем обе части последнего равенства по аргументу x, учитывая, что
. Продифференцируем обе части последнего равенства по аргументу x, учитывая, что 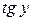 – сложная функция, так как
– сложная функция, так как 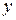 зависит от
зависит от 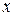 .
.
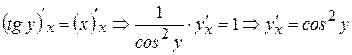
Далее выразив 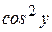 из соотношения
из соотношения 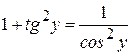 , получим
, получим 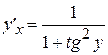 , а так как
, а так как 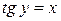 , а
, а 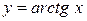 , то
, то
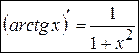 . (12)
. (12)
Для функции 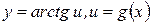 , используя правило дифференцирования сложной функции имеем:
, используя правило дифференцирования сложной функции имеем:
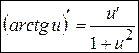 . (12’)
. (12’)
4 Теперь найдем производную функции 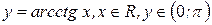 . Из определения арккотангенса имеем
. Из определения арккотангенса имеем 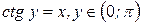 . Продифференцируем данное равенство по аргументу
. Продифференцируем данное равенство по аргументу 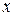 , учитывая, что
, учитывая, что 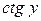 – сложная функция, так как
– сложная функция, так как 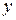 зависит от
зависит от 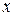
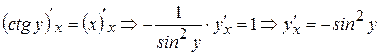
Далее выразив 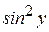 из соотношения
из соотношения 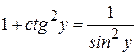 , получим
, получим 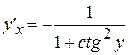 , а так как
, а так как 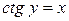 , а
, а 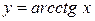 , то
, то
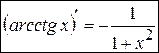 . (13)
. (13)
Для функции 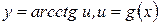 , используя правило дифференцирования сложной функции имеем:
, используя правило дифференцирования сложной функции имеем:
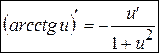 . (13’)
. (13’)
Примеры: Найти производные следующих функций:
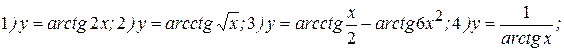
Решение:
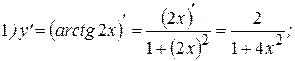
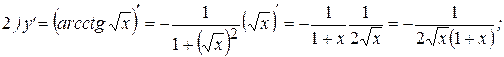

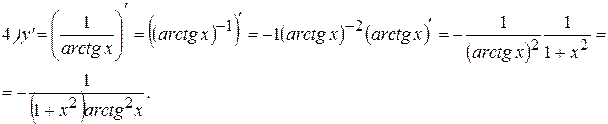
Упражнения: Найти производные следующих функций:
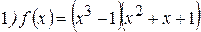
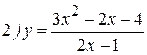
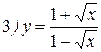
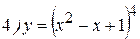
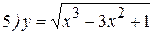
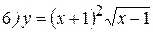
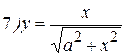
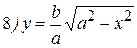
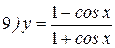
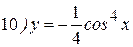
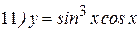
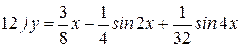
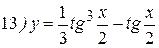
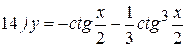
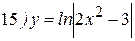
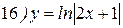
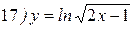
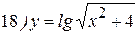
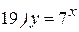
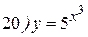
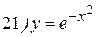
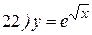
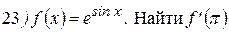
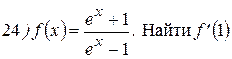
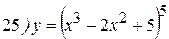
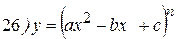
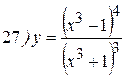
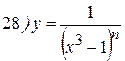
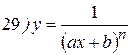
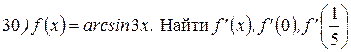
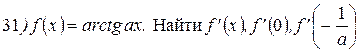
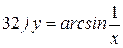
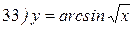
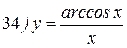
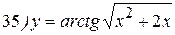
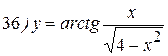
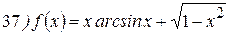
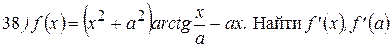
Теперь все доказанные нами формулы занесем в таблицу.
Таблица производных
1 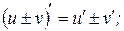 | |
2 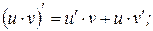 | |
3 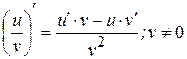 ; ; | |
4 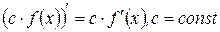 ; ; | |
5 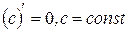 ; Для простых функций ; Для простых функций | Для сложных функций |
6 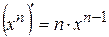 ; ; | 1 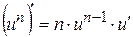 |
7 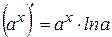 | 2 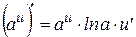 |
8 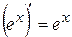 | 3 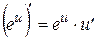 |
9 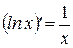 | 4 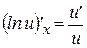 |
10 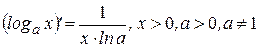 | 5 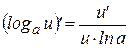 |
11 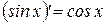 | 6 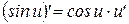 |
12 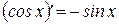 | 7 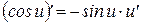 |
13 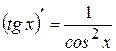 | 8 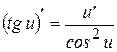 |
14 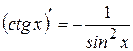 | 9 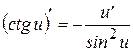 |
15 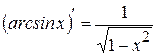 | 10 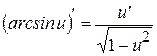 |
16 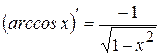 | 11 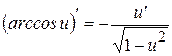 |
17 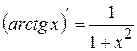 | 12 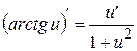 |
18 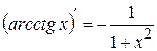 | 13 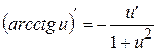 |
 2015-05-30
2015-05-30 6597
6597
