2015-05-30
342
ЧАСТНЫЕ СЛУЧАИ А) Если плоскопараллельное движение осуществляется путём качения без скольжения одного цилиндрического тела по поверхности другого, причём второе тело неподвижно, то точка касания имеет в данный момент времени скорость, равную нулю, и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу. Б) Если скорости точек А и В тела параллельны друг другу, причём линия АВ не перпендикулярна к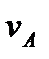 
, то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны 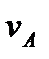. При этом из теоремы о проекциях скоростей следует, что 
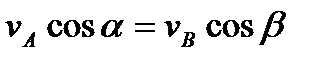, т.е. 
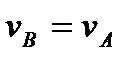; аналогичный результат получается для всех других точек тела. Следовательно, в рассматриваемом случае скорости всех точек тела в данный момент времени равны друг другу и по модулю, и по направлению, т.е. тело имеет мгновенное поступательное распределение скоростей. Угловая скорость тела в этот момент времени равна нулю. В) Если скорости точек А и В тела параллельны друг другу и при этом линия АВ перпендикулярна к 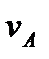, то мгновенный центр скоростей Р определяется построением…В этом случае нужно ещё знать направление и модуль скоросте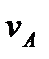й 
и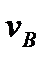 
. Г) Если известен вектор скорости 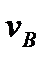какой-нибудь точки сечения S и угловая скорость 
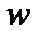, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к 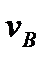, можно найти из равенства 
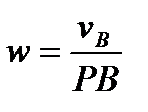которое даёт 
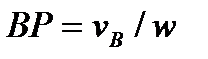. 1) Вычисляем величину угла 
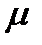из формулы 
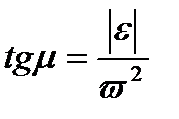. 2) От точки А под углом 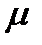к вектору 
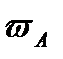проведём прямую AE, при этом прямая AE должна быть отклонена от 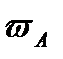в сторону вращения тела, если вращение является ускоренным, и против вращения, если оно является замедленным, т.е. в сторону напрвления углового ускорения 
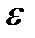. 3) Откладываем вдоль линии АЕ отрезок AQ, равный 
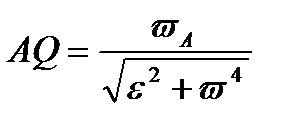. Построенная таким образом точка Q и будет мгновенным центром ускорений.
|
|
|
