2015-05-30
1032
Величина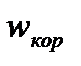 
, характеризующая изменение вектора относительной скорости 
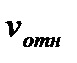в переносном движении и вектора переносной скорости 
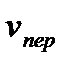в относительном движении, называется поворотным или кориолисовым ускорением точки. 
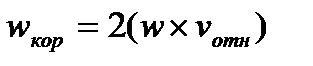, где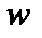 
- угловая скорость переносного движения, таким образом, кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки. Если угол между векторам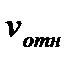и 
и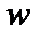 
обозначить через 
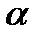, то по модулю 
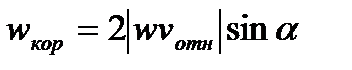. Напрвлен вектор 
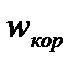так же, как вектор 
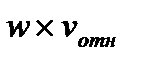, т.е. перпендикулярно плоскости, проходящей через векторы 
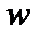и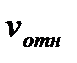 
в ту сторону, откуда кратчайшее совмещение 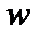с 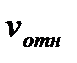видно происходящим против хода часовой стрелки. Кориолисово ускорение может обращаться в нуль в следующих случаях: 1) Когда 
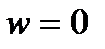, т.е. когда переносное движение является поступательным или если угловая скорость переносного вращения в данный момент времени обращается в нуль.; 2) Когда 
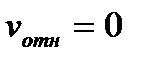, т.е. когда относительная скорость в данный момент времени обращается в нуль.; 3) Когда 
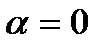, или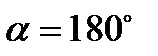 
, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения или если в данный момент времени вектор 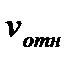параллелен этой оси. 
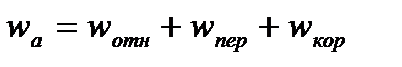- теорема Кориолиса: абсолютное ускорение точки равно геометрической сумме трёх ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении.
|
|
|
