Аппроксимация градиента давления

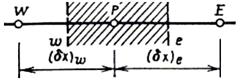
Рис. 6.1 3-хточечный шаблон (заштрихованная область - КО)

При составлении дискретного аналога уравнения количества движения в направлении оси x для одномерного случая, показанного на рис. 6.1, единственной особенностью является представление члена –дp/дx, проинтегрированного по КО.

В результате интегрирования в дискретный аналог войдет разность давления p_w-p_e, которая представляет собой силу давления, приложенную к КО с единичной площадью поперечного сечения.

.

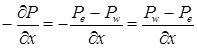Чтобы выразить p_w-p_e через давления в узловых точках, можно предположить, что давление между узловыми точками изменяется по линейному закону. Если грани КО e и w выбраны так, что они лежат посередине между соответствующими узловыми точками, то можно записать

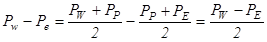(6.1)

Таким образом, дискретный аналог уравнения количества движения будет содержать разность давлений между двумя не соседними точками. Это означает, что давление берется с сетки более грубой чем основная, и это должно привести к снижению точности решения. Второй недостаток - лучше виден из рис. 6.2, на котором поле давления представлено через его значения в узловых точках.

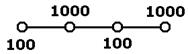Рис. 6.2 «Зигзагообразное» поле давления

При этом для каждой узловой точки P выражения для градиента давления будет выполнятся условие: PW-PE=0. Т.е. волнистое поле давления будет восприниматься в уравнении количества движения как однородное.

Эта трудность еще более усугубляется в 2D (а тем более 3D) случае. Так же как на количество движения в направлении оси x влияет перепад давления P_W-P_E, на количество движения в направлении оси y влияет перепад давления P_S-P_N, при этом значение давления в точке P не играет никакой роли (см. рис. 6.3).

Рис. 6.3 Шахматное поле давления

Имея это в виду, можно сделать вывод о том, что показанное на рис. 6.3 поле давления, образованное из расположенных в шахматном порядке четырех произвольных значений давления, не даст силу давления в направлениях осей x или y.

Таким образом, при рассмотренном способе дискретизации уравнений количества движения сильно неоднородное поле давления будет восприниматься как однородное. Если бы в процессе итерационного решения возникли такие поля давления, они бы не сохранились в процессе, так как уравнения количества движения «забудут» об этих полях.

Естественно, что численный метод, который допускает такие абсурдные решения, нежелателен.