Описанные выше трудности можно преодолеть, если понять что не обязательно рассчитывать все переменные в одних и тех же узловых точках. Можно по желанию использовать для каждой зависимой переменной свою сетку. При расчете составляющих скорости значительную выгоду дает определение их на сетке, отличной от сетки, которая используется для всех других переменных. Смещенная или шахматная сетка для расчета составляющих скорости впервые была использована в 1965 г. Использование такой сетки лежит в основе процедур SIVA и SIMPLE.
При расположенной в шахматном порядке сетке составляющие скорости рассчитываются для точек, лежащих на гранях контрольных объемов. Таким образом, составляющая скорости u вдоль оси x рассчитывается на гранях, перпендикулярных направлению оси x. Точки, в которых определяется u, показаны на рис. 6.5 стрелками, а узловые точки (назовем их основными) изображены кружками.
На рис. 6.6 показана двухмерная сетка, где узловые точки для u и v помещены на соответствующих гранях КО. Точно таким же образом можно сконструировать соответствующую трехмерную сетку.
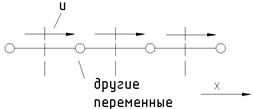
Рис. 6.5 Расположение u в шахматном порядке: горизонтальные стрелки - места определения u, точки - места определения других параметров.
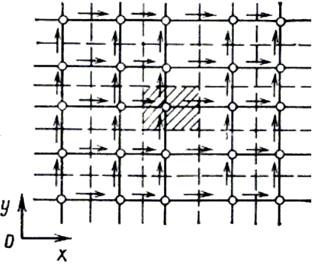
Рис. 6.6 Расположение u и v в шахматном порядке: горизонтальные стрелки - места определения u, вертикальные стрелки - места определения v, точки - места определения других параметров.
Прямым следствием введения шахматной сетки является то, что массовый расход через грани КО можно теперь определять без интерполяции соответствующей составляющей скорости (запись массовых расходов F).
Достоинства:
1. Для типичного КО дискретный аналог уравнения неразрывности содержит разности составляющих скорости в соседних точках, а это приводит к тому, что волнистое поле скорости (см. рис. 6.4) не будет удовлетворять уравнению неразрывности (при использование шахматной сетки только физичные поля скорости могут удовлетворять уравнению неразрывности).
2. Разность давлений между двумя соседними узловыми точками определяет составляющую скорости в точке, расположенной между этими узловыми точками (т.е. поля давления, показаны на рис. 5.2 и 5.3, не будут восприниматься как равномерные и не могут использоваться как возможные решения).
Следует учесть, что при использовании шахматном сетки надо предусмотреть в программе соответствующую индексацию и хранение геометрической информации, связанной с расположением узловых точек для составляющих скорости, а также дополнительную интерполяцию результатов.
Однако преимущества использования такой сетки намного превосходят дополнительные сложности.
 2015-05-30
2015-05-30 1823
1823








