Аналогичная трудность возникает при построении дискретного аналога уравнения неразрывности. Для стационарного одномерного течения жидкости с постоянной плотностью уравнение неразрывности имеет вид
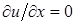 (6.2)
(6.2)
Проинтегрировав это уравнение по изображенному на рис. 6.1 КО, получим
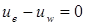
Так же как и ранее используя кусочно-линейные профили для u и располагая грани КО посередине между узловыми точками, получаем
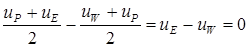 (6.3)
(6.3)
Итак, аппроксимация уравнения неразрывности привела к приравниванию скоростей в чередующихся узловых точках, а не в соседних (аналогично давлению).
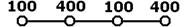 Рис. 6.4 Волнистое поле скорости Рис. 6.4 Волнистое поле скорости | В результате дискретному аналогу (6.3) уравнения неразрывности может удовлетворять нефизичное поле скорости (рис. 6.4). |
Аналогичные картины полей всех составляющих скорости можно составить для двух- и трехмерных случаев. Они будут удовлетворять уравнению неразрывности, но вряд ли могут быть получены как имеющие физический смысл решения задачи.
Эти трудности надо исключить до формулировки численного метода решения задачи в переменных, включающих составляющие скорости и давление. Прежде чем перейти к изложению способа преодоления указанных трудностей, отметим, что сложности численного анализа связаны, по-видимому, с первыми производными. Поведение вторых производных обычно не создает сложностей.
 2015-05-30
2015-05-30 1160
1160
