Для уравнения количества движения Ф обозначает одну из составляющих скорости и коэффициенту Г и свободному члену S следует придать соответствующий смысл. При использовании шахматной сетки дискретные аналоги уравнений количества движения несколько отличаются от дискретных аналогов уравнений для других Ф, рассчитываемых в узлах основной сетки. Однако это отличие относится к несущественным деталям. Оно связано с использованием для аппроксимации уравнений количества движения КО на шахматной сетке. КО для уравнения количества движения в направлении оси x показан на рис. 6.7. Если иметь в виду точки для нахождения только составляющей u, в этом КО нет ничего необычного.
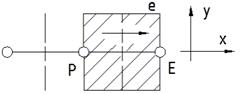 Рис. 6.7 КО для u: горизонтальные стрелки - места определения u, точки - места определения других параметров Рис. 6.7 КО для u: горизонтальные стрелки - места определения u, точки - места определения других параметров | Его грани лежат между точкой e и соответствующими соседними точками для u. Однако он смещен по отношению к обычному КО, расположенному вокруг основной узловой точки Р. Смещение объема произошло только в направлении оси x таким образом, что перпендикулярные этому направлению грани проходят через основные узловые точки P и E. |
Отсюда видно одно из главных достоинств шахматной сетки: разность pP-pE, можно использовать для расчета силы давления, действующей на КО для скорости u. Для расчета коэффициента диффузии и массового расхода на гранях КО, показанного па рис. 6.7, потребуется соответствующая интерполяция. Результирующий дискретный аналог можно записать в виде
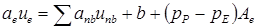 . (6.4)
. (6.4)
Здесь число соседних членов anbunb зависит от размерности задачи. Для двухмерной задачи - четыре точки вне КО; в трехмерном случае войдут шесть соседних значений u. Значения коэффициентов anb связаны с влиянием совместных конвективных и диффузионных процессов на гранях КО.
Член b определяется так же, как и ранее, но градиент давления не включен в составляющие источникового члена SC или SP. С градиентом давления связан последний член в (6.4). Так как требуется определить поле давления, было бы нецелесообразно включать давление в источниковый член уравнения количества движения.
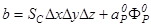
Член (pP-pE)Ae представляет собой силу давления, действующую на КО для u, а Ae - площадь поверхности, на которую действует этот перепад давления. В двухмерном случае Ae=Dy·1, в трехмерном Ae= Dy Dz.
Уравнения количества движения в других направлениях аппроксимируются таким же образом. На рис. 6.8 показан КО для уравнения количества движения в направлении оси y он смещен вдоль оси y. Дискретный аналог будет иметь вид
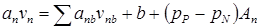 ,
,
где (pP-pN)An - соответствующая сила давления. В трехмерном случае аналогичное уравнение можно записать для составляющей скорости w.
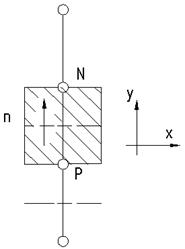 Рис. 6.8 КО для v: вертикальные стрелки - места определения v, точки - места определения других параметров. Рис. 6.8 КО для v: вертикальные стрелки - места определения v, точки - места определения других параметров. | Уравнения количества движения можно решить только в том случае, если поле давления задано или каким-то образом найдено. Если при решении использовать неверное поле давления, найденное поле скорости не будет удовлетворять равнению неразрывности. Выразим такое поле скорости, полученное с использованием приближенного поля давления p *, через u*, v*, w*. Это поле скорости находится в результате решения следующих уравнений: 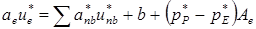 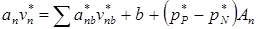 (6.5) (6.5) 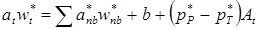 В этих уравнениях составляющим скорости и давлению приписан верхний индекс *. Отметим, что точка t лежит на сеточной линии, направленной вдоль оси z и проходящей через узловые точки Р и Т. В этих уравнениях составляющим скорости и давлению приписан верхний индекс *. Отметим, что точка t лежит на сеточной линии, направленной вдоль оси z и проходящей через узловые точки Р и Т. |
 2015-05-30
2015-05-30 1059
1059
