2015-05-30
1164
Преобразуем уравнение неразрывности в уравнение для поправки давления. Предположим, что плотность r непосредственно не зависит от давления. Смысл этого предположения будет рассмотрен ниже. Вывод уравнений проведен для 3D случая. Легко можно получить уравнения также для 1D и 2D случаев.
Уравнение неразрывности имеет вид
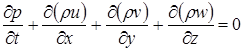. (6.13)
Проинтегрируем это уравнение по показанному на рис. 6.9 заштрихованному КО (на рис. 6.9 показано только 2D сечение). Напомним, что такой КО использовался при выводе дискретного аналога уравнения для обобщенной переменной Ф.
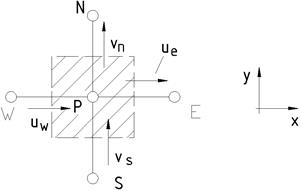
Рис. 6.9. КО для уравнения неразрывности: горизонтальные стрелки - места определения u, вертикальные стрелки - места определения v, точки - места определения других параметров
При интегрировании члена dp/dt предположим, что значение плотности во всем КО равно rP. Также будем считать, что значение массовой скорости на всей грани КО определяется значением составляющей скорости ue в точке е.
В соответствии с полностью неявной аппроксимацией предположим, что новые значения скорости и плотности (в момент времени t+Dt) преобладают на всем шаге по времени; старое значение плотности rP0 (в момент времени t) будет входить только из-за наличия члена dp/dt. В этих предположениях интегрирование уравнения (6.13) дает (6.14)
|
|
|
.
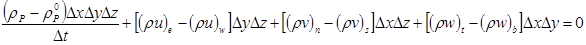Если, теперь вместо всех составляющих скорости подставить их выражения из поправочных формул для скорости (6.10)-(6.12), то после группировки соответствующих членов поручим следующее уравнение для сеточных значений p':
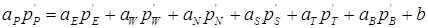, (6.15)
где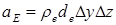 
, 
, 
,
, 
, 
,
, 
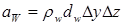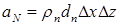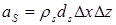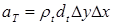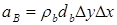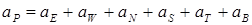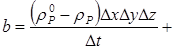
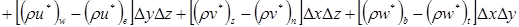
Так как значения плотности r определены, вообще говоря, в узловых точках основной сетки, ее значения на границах, такие, как re, можно рассчитать с помощью подходящей интерполяции. Независимо от применяемого способа интерполяции значения re для двух КО, имеющих общую грань, должны быть согласованы между собой.
Из (6.15) можно видеть, что член b уравнения для поправки давления по существу равен (со знаком минус) левой части дискретного аналога уравнения неразрывности (6.14), записанного через значения составляющих скорости с индексом *.
Равенство b=0 означает, что эти составляющие вместе с имеющимся значением (rP0-rP) удовлетворяют уравнению неразрывности и не требуется никакой коррекции давления. Таким образом, член b представляет собой «источник массы», который должен быть скомпенсирован поправками давления (через соответствующие поправки скорости).
Итак, мы получили все уравнения, необходимые для определения составляющих скорости и давления. Теперь можно рассмотреть весь алгоритм решения в целом.
