Определение.
Пусть задано некоторое непустое множество Х. Непустое семейство 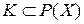 называется кольцом, если оно обладает тем свойством, что из А
называется кольцом, если оно обладает тем свойством, что из А 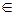 K и В
K и В 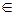 K следует А
K следует А 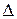 В
В 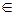 K, А È В
K, А È В 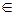 K.
K.
Определение.
Кольцо K называется алгеброй, если Х 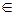 K. Х в этом случае называется единицей кольца. Примеры:
K. Х в этом случае называется единицей кольца. Примеры:
1) Для любого множества X система P(X) всех его подмножеств представляет собой алгебру множеств.
2) На числовой прямой R система его конечных и счетных подмножеств представляет собой кольцо, но не алгебру.
Определение.
Пусть на некотором множестве Х задано полукольцо S 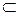 Р (Х). Будем говорить, что на S задана мера, если каждому элементу А
Р (Х). Будем говорить, что на S задана мера, если каждому элементу А 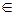 S поставлено в соответствие вещественное число m (A)
S поставлено в соответствие вещественное число m (A) 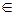 R таким образом, что выполнены следующие условия:
R таким образом, что выполнены следующие условия:
1) 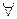 A
A 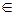 S: m (A)
S: m (A) 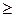 0;
0;
2) если 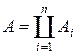 , A, Ai
, A, Ai 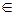 S, то
S, то 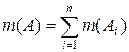 .
.
 2015-05-22
2015-05-22 541
541







