Определение интегрируемой по Лебегу измеримой функции. Примеры интегрируемых и не интегрируемых по Лебегу функций

Определение:

Назовем измеримую функцию 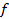суммируемой по мере µ (интегрируемой по Лебегу) на X, если существует последовательность простых суммируемых на X функций 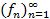, равномерно сходящаяся к 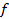. Интегралом Лебега суммируемой функции 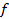на множестве X называется предел интегралов Лебега от простых суммируемых функций :

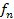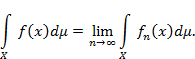
Это определение корректно, если выполнены следующие условия:

1)Предел для любой равномерно сходящейся последовательности простых суммируемых на X функций существует.

2)Этот предел при заданной функции 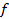не зависит от выбора последовательности .

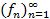3)Для простых функций определения совпадают.