Определение и примеры измеримых функций

Множество X, на котором задана некоторая σ-алгебра его измеримых подмножеств Σ называется измеримым пространством и обо-значается (X; Σ).

Пусть X – пространство с мерой. Действительная функция f: X → R называется измеримой, если для любого c 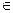R множество A_c = {x: f (x) < c} измеримо (здесь R – расширенная

числовая прямая). Комплекснозначная функция g + ih измерима, если измеримы ее действительная и мнимая части.

Определение и примеры простых функций.

Пример:

Определение интеграла Лебега для простой функции. Примеры интегрируемых и не интегрируемых по Лебегу простых функций.

Пример неинтегрируемой функции:

Пример интегрируемой(можно придумать самому).