Определение множества (ограниченного) на числовой прямой, измеримого по Лебегу. Примеры измеримых по Лебегу множеств на прямой

Пусть m – полная, счётно-аддитивная, конечная мера. Множество 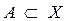называется измеримым по Лебегу относительно меры m, заданной на алгебре множеств К, если выполняется равенство: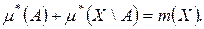

Пусть 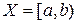– некоторый фиксированный полуинтервал прямой, 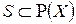– полукольцо, состоящее из полуинтервалов 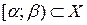. Пусть K – алгебра подмножеств, порождённая полукольцом S, каждый элемент которой имеет вид 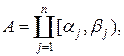причём полуинтервалы в правой части попарно не пересекаются. Через m обозначим меру на алгебре K, полученную продолжением меры с полукольца, т.е. 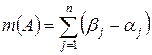. Для произвольного множества 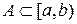определим внешнюю меру 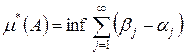, где точная нижняя грань берётся по всем таким наборам полуинтервалов 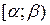, что 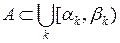. Множество 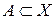называется измеримым по Лебегу, если 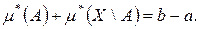Таким образом, мерой Лебега m на отрезке называется лебеговское продолжение длины.

Примеры:

Рассмотрим измеримые по Лебегу линейные ограниченные множества:

1)множество, состоящее из одной точки, измеримо и его мера равна нулю;

2)всякое не более чем счётное ограниченное множество точек прямой измеримо и его мера равна нулю;

3)любой промежуток измерим и его мера равна его длине;

4)любое ограниченное открытое или замкнутое множество измеримо по Лебегу;

5)любое ограниченное борелевское множество на прямой измеримо по Лебегу.