Основные определения. Развитие математики привело к острой необходимости единого описания результатов расчетов, при которых требуется вычисление радикалов четных степеней типа и

Развитие математики привело к острой необходимости единого описания результатов расчетов, при которых требуется вычисление радикалов четных степеней типа 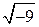и т.п. Известные числовые множества от N до R исключают такую операцию, объявляя невозможным решение уравнений типа х² + 9 = 0. Для возможности хотя бы формальной записи решения введем понятие мнимой единицы i, определяемой своим основным свойством i² = -1. Тогда радикал 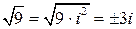. Т.е., с помощью i становится возможным представление любых четных корней из отрицательных чисел. Последовательные степени мнимой единицы имеют вид:

i, i²= -1, i³=i² i=-i, i⁴=i² i² = 1, i⁵ =i⁴ i=i,..., i⁴ⁿ⁺¹=i, i⁴ⁿ⁺²= -1, i⁴ⁿ⁺³=-i, i⁴ⁿ= 1,

где .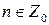

Комплексным числом называется выражение z = a + b i, где 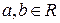, а - действительная (вещественная) часть, b - мнимая часть.

Заметим, что при b = 0 комплексное число преобразуется в действительное, т.е. 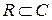. Если а = 0, то z = 0 + bi = bi называется чисто мнимым числом.

Часто комплексные числа записываются в виде упорядоченной пары (кортежа) действительных чисел, т.е. z= a + bi = (а; b).