В классической четкой (двухзначной) логике существуют логические операции «И», «ИЛИ», «НЕ», которые определяются единственным образом и они составляют полные системы, т.е. любое уравнение четкой логики путем логических преобразований может быть выражено в виде логических комбинаций:
«не-и-или»;
«не-и»;
«не-или».
Одна из задач теории нечетких множеств состоит в обобщении четких логических операций в их нечеткие аналоги. Нечетким расширением операции «и» в общей форме является Т или триангулярная норма, которая в теории нечетких множеств обозначается символом (Т).Другим названием Т-нормы является S-конорма [9].
Эта операция определяется как отображение:
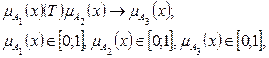
для которого выполняются аксиомы:
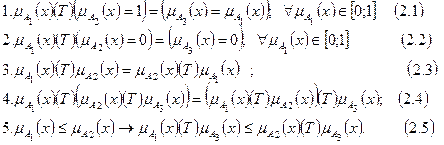
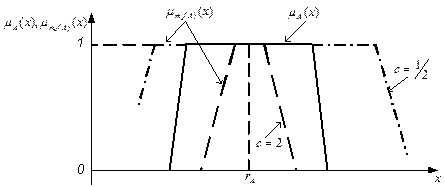
|

|

| |||
|
аксиомы (2.1),(2.2) называются аксиомами граничных условий Т-нормы; (2.3),(2.4) – объединения или пересечения, (2.5)- упорядоченности.
На схемотехническом уровне операция (T) реализуется в виде схемы с двумя входами и одним выходом (рис.2.1). Аксиомы (2.3),(2.4) означают, что входы равнозначны и нет необходимости их различать. С позиций традиционной математики операция (T) реализует функцию двух переменных:
y=Т(u1,u2),
где 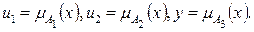
Эта функция «Т» в трехмерном пространстве (u1,u2,y) изображает некоторую поверхность. Геометрическая фигура, построенная в соответствии с аксиомами граничных условий, дает возможность определить максимальные и минимальные значения Т-нормы, как функции двух переменных. При ее построении величинам
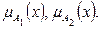
придают различные значения, принадлежащие отрезку [0;1], и в соответствии с (2.1), (2.2) определяют значение
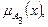
что в системе координат (u1,u2,y) дает соответствующую совокупность точек (рис.2.2)
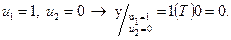
Это изображает точку А1 с координатами (u1=1; u2=0; y=0).
После аналогичных вычислений получаются координаты точек А2-А4:
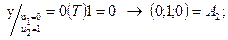
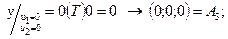
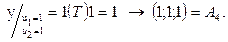
Совокупность точек А2-А4 определяют вершины единичного куба. При изменении u1 от 0 до 1 и фиксированном u2=1 получим уравнение прямой В1:
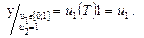
Далее аналогично для прямых В2-В4:
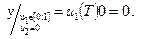 - уравнение прямой В2
- уравнение прямой В2
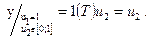 - уравнение прямой В3
- уравнение прямой В3
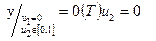 - уравнение прямой В4.
- уравнение прямой В4.
Из аксиомы 3 (2.3) имеем:
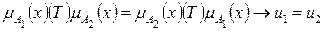 - уравнение плоскости С1.
- уравнение плоскости С1.
Таким образом, максимальные и минимальные значения Т-нормы изображаются геометрической фигурой симметричной относительно плоскости u1-u2=0.
В теории нечетких множеств в зависимости от способов задания операции (Т), которые удовлетворяют аксиомам (2.1)-(2.5), существует бесконечное число нечетких операций «и». В теории нечеткого управления находят применение следующие их типы.
Логическое произведение (Заде,1973 г.):
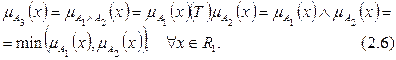
Можно показать, что аксиомы (2.1)-(2.5) для операции «Ù» выполняются.
Геометрическая фигура граничных условий для логического произведения получается по методике аналогичной выше и в результате будем иметь совокупность точек А1-А4 и прямых В1-В4.
По аксиоме (2.3) получим уравнение прямой В5, проходящей через т. А3=(0,0,0) и т. А4=(1,1,1) (рис.2.3):
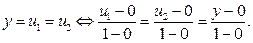
Логическое произведение (2.6) имеет геометрическую интерпретацию в виде пересечения нечетких множеств А1 и А2 (рис.2.4).
Алгебраическое произведение (Бандлер и Кохоут,1980):
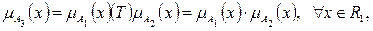 (2.7)
(2.7)
где символ «×» – произведение, принятое в классической алгебре. Выполнение аксиом (2.1)-(2.5) очевидно. График граничных условий Т-нормы для т.т. А1-А4, прямых В1-В4 получается аналогично предыдущему. Найдем уравнение кривой В5.
Из (2.3):
y=u1×u2= u2×u1
следует, что u1=u2, поэтому
y=u12= u22.
При 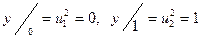 . В результате сложении этих уравнений получим:
. В результате сложении этих уравнений получим:
u12+ u22=1, откуда 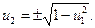
Так как u2³0, поэтому 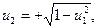
определяет уравнение кривой В5, проходящей через т.т. А1,А2 (рис. 2.5).
Геометрическая интерпретация алгебраического произведения (2.7) изображена на рис.2.6.
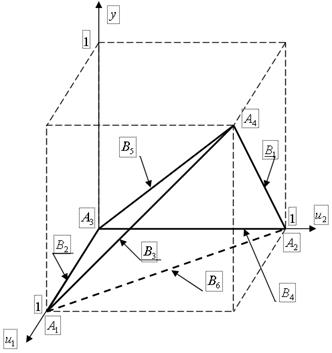
Рис.2.3. Граничные условия логического произведения.
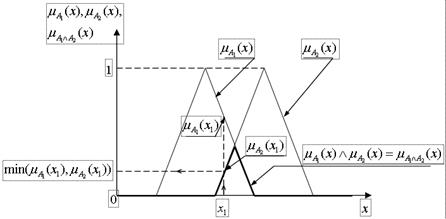
Рис.2.4. Логическое произведение нечетких множеств.
Граничное произведение (Лукашевич, Гилес, 1976):
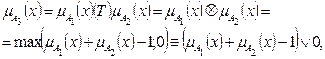 (2.8)
(2.8)
где символ Ä - граничное произведение). График граничных условий аналогичен предыдущему (совокупность т.т. А1-А4 и прямых В1-В4). Кривая В6 из (2.3) имеет вид:
y=u1Äu2= u2Äu1®(u1+u2-1)Ú0=0Ú(u1+u2-1) ® u1+u2-1=0®
®u2=1-u1.
Геометрическая интерпретация (2.8) приведена на рис. 2.6.
Сильное или драстическое (drastic) произведение (Вебер,1983):
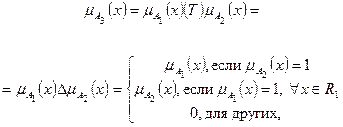 (2.9)
(2.9)
где D - символ сильного произведения. Геометрическая интерпретация (2.9) изображена на рис 2.6.
Из графических построений следует, что справедливо соотношение:
0£u1Du2£u1Äu2£ u1×u2£ u1Ùu2.
Существует бесконечное число других типов нечеткой операции «и». Некоторые из них, зависящие от вещественных параметров, приведены в [6].
В теории нечетких множеств показывается, что все операции «и» расположены между сильным и логическим произведениями:
0£u1Du2£…… u1Ùu2.

|
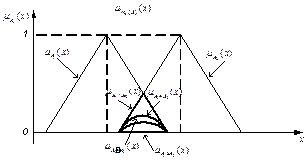
|
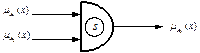
|
 2015-05-22
2015-05-22 1443
1443

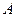 (тело), модифицированные нечеткие множества «очень(
(тело), модифицированные нечеткие множества «очень(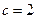 ) и «более или менее(
) и «более или менее(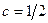 ), полученные путем изменения масштаба относительно точки
), полученные путем изменения масштаба относительно точки 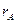 .
.