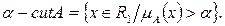
Из определений следует
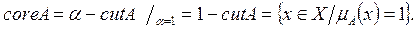
|
|
|
|
|
|
|

|
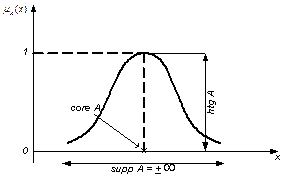
т.е. ядро нечеткого множества равно разрезу с a = 1
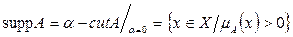
т.е. основание нечеткого множества равно разрезу с 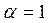 .
.
Выпуклое (convex) нечеткое множество А:
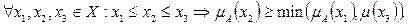
При невыполнении неравенства нечеткое множество называется невыпуклым.
Нечеткое разбиение нечеткого множества А. Если имеем: нечеткое множество А; нечеткие подмножества
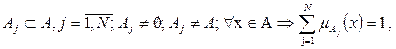
тогда подмножества А 1, …, А N называются нечетким разбиением нечеткого множества А.
Пример. Пусть 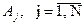 нечеткие подмножества, такие что
нечеткие подмножества, такие что
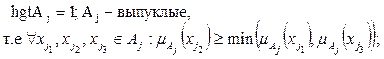
для " j нечеткое подмножество не содержит более 2-х пересечений с другими нечеткими подмножествами, тогда Aj есть нечеткое разбиение А (рис.1.18).
Специальный тип нечеткого множества А называется нечетким числом, если выполняются следующие условия:
А является выпуклым, (1.5)
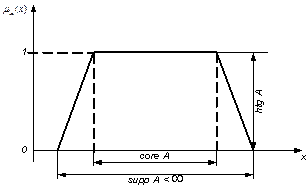
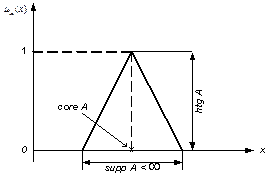
А является нормальным (hgt A =1), (1.6)
mA(x) является кусочно-непрерывной функцией, (1.7)
core A содержит одну точку. (1.8)
Пример нечеткого числа «приблизительно 5» в графической форме приведен на рис.1.19.
Нечеткое множество А, для которого выполняются условия (1.5) – (1.7), а (1.8) не выполняется, называется нечетким интервалом. Пример нечеткого интервала «от приблизительно 2 до приблизительно 7» приведен на рис.1.20.
Рис.1.18. Нечеткое разбиение нечеткого множества. 
Рис.1.19. Нечеткое число « 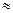 5».
5». 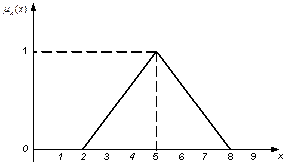
Рис.1.20. Нечеткий интервал «от приблизительно 2 до приблизительно 7». 
Рис.1.20. Нечеткий интервал «от приблизительно 2 до приблизительно 7».
1.3. Принцип обобщения.
Этот принцип обобщает понятие «отображение» математического анализа и соответственно математические операции типа сложение, вычитание, умножение, деление и другие, которые в теории нечетких множеств интерпретируются как специальный тип отображения. Впервые этот принцип был сформулирован Л.Заде в 1975 году и является одним из наиболее важных в теории нечетких множеств. Как утверждают ведущие специалисты в области теории нечетких множеств Дубоис (Dubois) и Праде (Prade) “этот принцип дает общий метод для обобщения нечетких понятий с тем, чтобы иметь дело с нечеткими количествами» [7].
Применение этого принципа для нечеткой арифметики с нечеткими числами позволяет решать традиционные задачи теории управления: параметрической и структурной идентификации; фильтрации и прогнозирования случайных процессов; обработки измерений по методу наименьших квадратов; распознавания образов и другие задачи.
Имеется много вариантов определения нечеткого отображения. Рассмотрим некоторые из них.
Классическое отображение ¦ определяется как соответствие элемента хÎА1 элементу уÎА2:
¦: А1® А2.
В теории нечетких множеств нечеткое отображение ¦ определяется, как соответствие элемента хÎА1 элементу уÎ 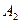 с
с  функцией принадлежности m ¦ (x,у). В одномерном случае нечеткое отображение в системе координат { x,у,m ¦ (x,у) } характеризуется некоторой поверхностью и для этого отображения приняты различные обозначения:
функцией принадлежности m ¦ (x,у). В одномерном случае нечеткое отображение в системе координат { x,у,m ¦ (x,у) } характеризуется некоторой поверхностью и для этого отображения приняты различные обозначения:
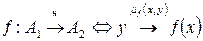
и т.д.
По другому варианту определения нечеткое отображение ¦ это отображение с нечеткой областью определения А1 и нечеткой областью значений А2:
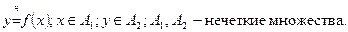
Иногда нечеткое отображение ¦ определяется нечеткой поверхностью m ¦ (x,у) в А1´А2.
Нечеткая функция ¦ многих переменных определяется в виде:
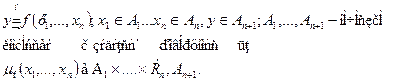
Геометрическая интерпретация нечеткой функции одного переменного 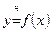 приведена на рис.1.21.
приведена на рис.1.21.
Принцип обобщения в многомерном случае формулируется в следующей постановке:
- задана нечеткая функция многих переменных 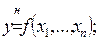
- задано нечеткое множество А аргумента нечеткой функции
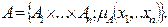
Необходимо найти функцию принадлежности 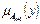 нечеткого множества Аn+1, которое является область значений нечеткой функции многих переменных
нечеткого множества Аn+1, которое является область значений нечеткой функции многих переменных
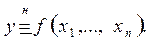 |
Имеет место следующее определение принципа обобщения в многомерном случае
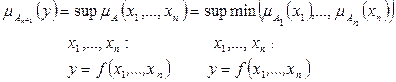
Пример. Применим этот принцип для сложения двух нечетких чисел:
«@5 + @2» с заданными непрерывными функциями принадлежности треугольного типа:
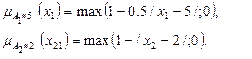
(1.9)
(1.10)
Шаг1. По заданным
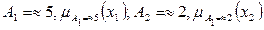
находятся (рис.1.22)
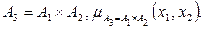
|
|

Шаг 2. Находится
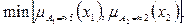 .
.

Для этого фиксируется х2=х21 и варьируется х1Î[3,7]. В результате получается плоскость p1, которая пересекает пирамиду
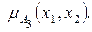
по прямой С1С2 (рис.1.23). Аналогично поступаем для х2=х21 и далее для х1=х11, х1=х12, ….. и т.д. В проекции на горизонтальную плоскость х2 0х1 при различных у={0;1/4;1/2;3/4;1} будем иметь изокривые (рис.1.24)
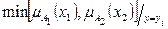 (1.11)
(1.11)
Шаг 3. На горизонтальной плоскости х2 0х1 строятся зависимости для отображения у=х1+х2 при фиксированных у=уi (рис.1.25)
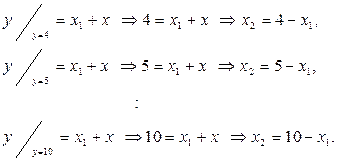
Пересечение этих прямых с изокривыми определяются точки:
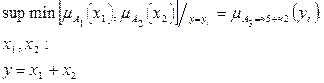
В результате получается совокупность точек (рис.1.26):
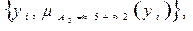
которые определяют функцию принадлежности при сложении двух нечетких чисел «»5+»2».
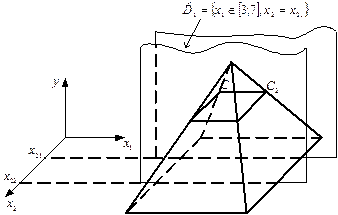
|

| |||
|
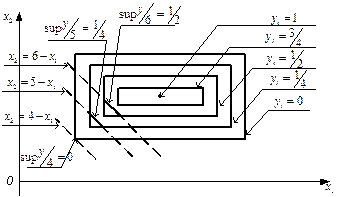
|
Аналогичные построения могут быть сделаны в случае арифметических операций «-» «:» «х» для нечетких чисел с треугольными функциями принадлежностей.
Пусть, как и ранее, имеем функции принадлежностей (1.9), (1.10) двух нечетких чисел»5 и»2 и необходимо вычислить»5-»2, т.е. необходимо найти:
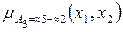 .
.
После вычисления прямого произведения пространств А3=А1хА2 и дальнейших построений, получим в плоскости х2х1 соответствующие изокривые (1.11), и, для задаваемых Сi, соответствующие зависимости у=х1-х2=Сi (рис.1.27). Их взаимные пересечения определяет совокупность:
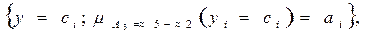
которая будет представлять собой функцию принадлежностей
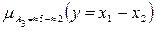
разности 2-х нечетких чисел «»5-»2».
На рис.1.28 показаны изокривые и зависимости у=х1 × х2=Сi, возникающие при вычислении «»5´»2». На рис. 1.29 представлены изокривые и зависимости
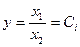
при вычислении «»5:»2».
|
|
|
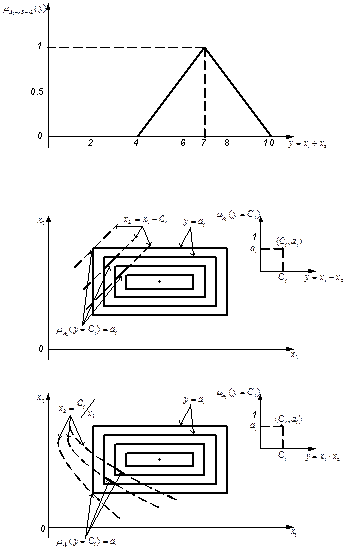
Геометрические построения, представленные на рис.1.22-1.29, показывают, что при наличии треугольных функций принадлежностей и элементарных арифметических операций типа «+», «-», «:», «´», получение результирующей функции принадлежностей является более или менее тривиальной операцией. В этом случае принцип обобщения для результирующей функции принадлежностей может быть сформулирован в виде следующего правила:
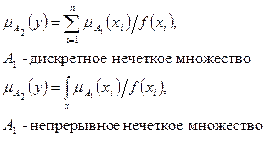 (1.12)
(1.12)
треугольными функциями принадлежностей.
Рассмотрим несколько примеров арифметических операций с нечеткими числами по (1.12.).
Пример. Имеем нечеткое число «»5» с дискретной функцией принадлежностей (рис.1.30):
m»5(х)=0.5¤4+1¤5+0.5¤6.
Это нечеткое число возводится в квадрат (»5)2=(»5)*(»5).
Необходимо найти m(»5)2(х).
|
|
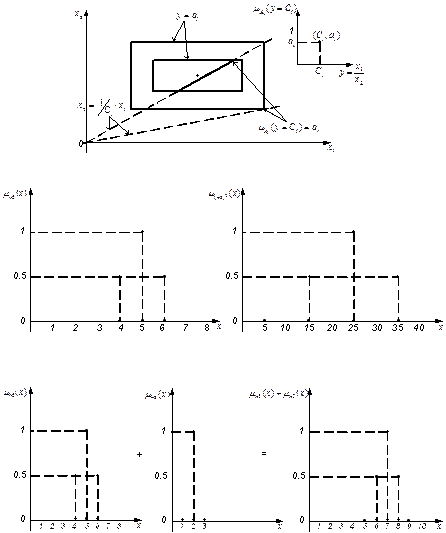
|
В соответствии с (1.12) имеем
3
m(»5)2 = S = m(»5)(xi)/ xi=(0,5/4+1/5+0,5/6)2=(0,5/42+1/52+0,5/62)=
=0,5/16+1/25+0,5/36.
Пример. Имеем нечеткие числа «»5» и «»2» с дискретными функциями принадлежностей (рис.1.31):
m»5=0,5/4+1/5+0,5/6; m»2(х)=1/2.
Рассматривается сумма 2-х нечетких чисел: «»5 +»2». Необходимо найти m»5 + »2(х). По (1.12) имеем:
m»5+ »2 (х)= (0,5/4+1/5+0,5/6)+ (1/2)=(0,5/4+2+1/5+2+0,5/6+2)= 0,5/6+1/7+0,5/8.
При наличии более сложных функций принадлежности, например, колоколообразных:
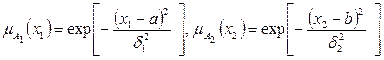
с показателями нечеткости d1,d2 соответственно, построение результирующей функции принадлежностей для соответствующих арифметических операций представляет собой достаточно сложную вычислительную процедуру (рис. 1.32). В некоторых случаях не всегда удается получить аналитические решения для результирующей функции принадлежностей. Это обусловлено вычислением декартового произведения пространств.

|
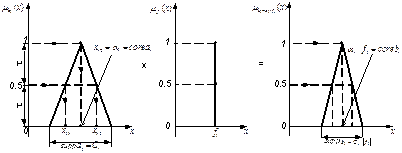
|
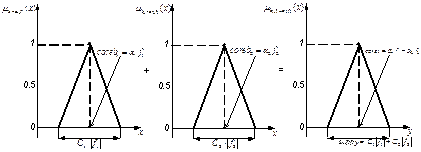
|
 2015-05-22
2015-05-22 820
820

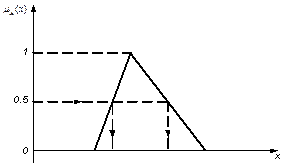
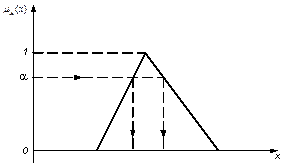
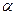 -уровень нечеткого множества.
-уровень нечеткого множества. 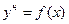 .
. 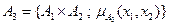 .
. 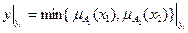 .
. 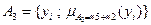 .
. 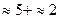 ».
». 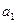 на четкое число
на четкое число 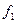 :
: 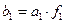 .
. 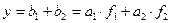 .
. 






