В теории нечетких множеств большинство арифметических операций определены для непрерывных областей. Операции для дискретных областей выделяются обычно в виде особого случая.
На практике нечеткие множества запоминаются в компьютере в виде данных о структуре и операциях над ними, и далее производится исполнение этих операций. Компьютерная реализация обуславливает необходимость рассмотрения основных форм представления нечетких множеств. Эти представления имеют три формы.
Функциональное (аналитическое) представление. Для представления нечеткого множества в этой форме используется представление в виде некоторой функциональной
зависимости ¦:
mА (х)=¦(х).
Примером ¦ служат зависимости треугольного (1.2), трапецеидального (1.3), колоколообразного (1.4) и других типов. При использовании такого представления появляются затруднения, обусловленные необходимостью производить операции с множеством другого типа представления, например, с дискретным нечетким множеством. При функциональном представлении возможно использование компьютера, оперирующего символами. Однако символьные вычисления возможны лишь для простых операций с простыми функциями принадлежностей. Во многих случаях результат не может быть представлен в символьной форме в виде функциональной зависимости, поэтому используются различные варианты приближения для результирующей функции принадлежностей. Таким образом, при компьютерном решении практических задач необходима дискретизация непрерывной области.
Парное представление. Оно определяется в виде
mА (х)= m1/x1+…..+mn/xn,
где xi – дискретные значения аргумента, mi – дискретные значения функции. Это представление описывает дискретные нечеткие множества. Примером такого описания в лингвистических переменных служит множество «друзья Петра», которое объединяет множество персон, определяемых своими именами xi и рангами mi, которые приписываются друзьям и эти ранги определяют степень дружбы.
Уровневое представление. Оно описывает нечеткое множество, как совокупность уровней или a сечений:
mА (х)=sup[a-cut(mА (х))],
aÎ(0,1]
где a- дискретное.
Во многих прикладных задачах возникает проблема сравнения нечетких чисел. Эта операция вводится следующим образом. Пусть имеем два нечетких числа хн и yн, что, согласно определению, означает то, что эти нечеткие числа имеют треугольные функции принадлежностей m(хн), m(yн). Представим нечеткие числа в уровневой форме, тогда будем иметь:
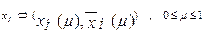
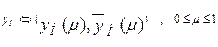
где ó - символ эквивалентности.
Для каждого нечеткого числа вводится критерий:
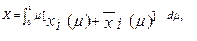
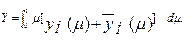
Полагается, что хн £ yн, если выполняется: X £ Y.
Таким образом, введенный критерий позволяет сравнить нечеткие числа. В частности, очевидно, что введенное упорядочивание обобщает обычную операцию «четких чисел». Можно показать, что введенное упорядочивание нечетких чисел является транзитивным и рефлексивным, т.е.:
- транзитивность R: хн, yн, zн из условий хн R yн, yн R zн, => хн R zн, где R – символ отношения упорядочивания (£, ³, =);
- рефлективность R: если хн R xн для " хн £ Xн, где Xн – совокупность нечетких чисел. Типичные примеры рефлексивности:подобие,тождественность, эквивалентность и т.д.
Пример. Определим отношение упорядочивания между нечетким числом»2 и нечетким числом»5.
Имеем:
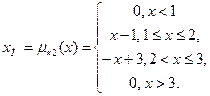
В уровневой форме хн соответственно будет иметь представление:
Хн = (m+1,3-m), 0 £ m £ 1. Далее пусть задано:
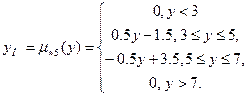
или в уровневой форме: yн = (2m+3,-2m+7), 0 £ m £ 1.
Критерий Х равен:
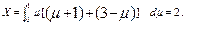
Для Y имеем:
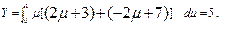
Из расчетов следует, что X = 2 < 5 = Y, поэтому»2 <»5.
Для компьютерной реализации в основном используется парное представление, а функциональное – лишь для компьютера, имеющего символьную форму операций.
Рассмотрим компьютерную реализацию перечисленных выше форм представления нечетких множеств.
Для приближенного описания функционального представления дискретным имеется несколько вариантов, каждый из которых имеет свои преимущества и недостатки.
Один из этих вариантов – это векторное представление, которое является дискретной аппроксимацией непрерывной области в виде парного представления с равноточной дискретной областью. Название такого вида представления связано с тем, что значения принадлежности в памяти компьютера запоминается как вектор. Например, при xÎ[0,10] и шаге D=1 дискретизации имеем:
10
mА (х)=max(1- ½ ×êx-5ê; 0)»Smi/i×D=
i=0
=(0/0+0/1+0/2+0/3+½/4+1/5+ ½/6+0/7+0/8+0/9+0/10=
=(0,0,0,0,½,1, ½,0,0,0,0).
В двумерном случае при х1,х2:0,1,2,3,…..10 имеем совокупность векторов или матрицу:
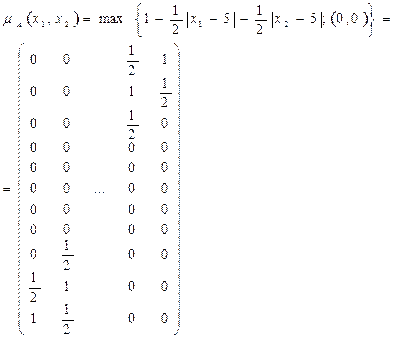
В трехмерном случае будем иметь соответственно совокупность матриц и т.д. Этот тип приближения может приводить к проблеме, когда необходимо представить четкое число в виде нечеткого множества. В этом случае нечеткое множество представлено только одной точкой (функция принадлежности – синглон), которая не подлежит какой-либо дискретизации, поэтому это множество не может быть представлено в векторной форме. В этом случае используется приближение для singl(x-xk) по двум соседним значениям mr,/xr, mi/xi какой-либо дискретной функции принадлежностей, которая находится в компьютерной памяти. Это приближение может быть получено из геометрических построений (рис.1.37). Пусть xk=mA-1(1) обозначает обратное отображение. Величина xk является неизвестной и подлежит определению. Пусть выбрано значение xr, тогда по заданному mА(х) определяется соответствующее значение mr и площадь S3=mr×xr. Значение mi выбирается из условия mi=1-mr, тогда соответственно
найдутся xi и площадь S4+ S2=mr×xi. Координата mi=1-mr находится из условия S1= S2:

|
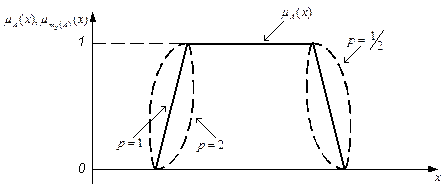
|
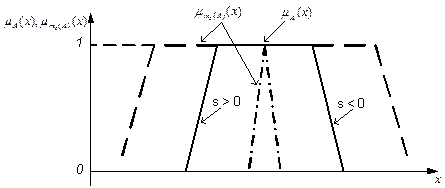
|
mr×[mA-1(1)- xr]= 1-mr×[ xi-mA-1(1)],
откуда получается: 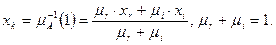
Таким образом, получено приближение четкого множества в виде нечеткого множества.
Парное представление в компьютере реализуется точечным способом. При этом шаг дискретизации необязательно представляется эквидистантным способом. Промежуточные значения получаются методом интерполяции. Этот способ имеет преимущества перед векторным представлением, т.к. при точечной реализации отсутствуют ограничения, связанные с эквидистантной дискретизацией. Точечный способ часто используется в программном обеспечении компьютеров при решении коммерческих задач методами нечеткого управления. Простым примером является нечеткое множество с треугольной функцией принадлежности, которая содержит только три точки mi/xi, а остальные получаются путем интерполяции. Более сложная форма может быть аппроксимирована любым способом, который дает компромисс между необходимой памятью и точностью.
Уровневое представление нечеткого множества в компьютере также реализуется путем дискретизации. При уровневой дискретизации нечеткое множество запоминается в виде множества интервалов, каждый из которых имеет свой вес. Каждый из этих интервалов является классическим четким множеством и включение их в нечеткое множество производится в соответствии со своим весом. При уровневой дискретизации возникает проблема, связанная с вычислением произведения пространств. Число операций над классическими множествами зависит экспоненциально от числа нечетких множеств, включенных в произведение пространств.
В программном обеспечении компьютеров обычно имеются различные способы представления нечетких множеств и, в зависимости от операций над ними используется та или иная форма представления. Например, при существовании решений для определенных типов операций в аналитической форме целесообразно использовать функциональное представление нечеткого множества.
 2015-05-22
2015-05-22 2794
2794

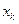 функции
функции 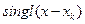 с соседними значениями
с соседними значениями 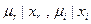 .
. 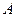 (тело), модифицированные нечеткие множества «очень(
(тело), модифицированные нечеткие множества «очень(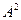 при
при 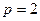 и «более или менее(
и «более или менее(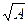 при
при 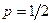 , для которых используется арифметическая операция возведения в степень.
, для которых используется арифметическая операция возведения в степень.