1.Любую неотрицательную случайную величину
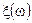
| Проверьте сходимость! | можно представить в виде предела последовательности простых случайных величин следующего вида |
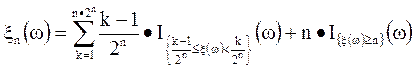
которая сходится к исходной случайной величине в каждой точке монотонно снизу
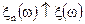
Так как любую случайную величину можно представить в виде разности ее положительной и отрицательной части
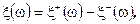
где
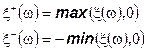
| Докажите! | которые также являются случайными величинами, |
и
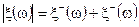
то сказанное выше относится (за исключением монотонности сходимости) к любой случайной величине, т.е.
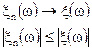
2.Более того, пусть
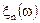
- сходящаяся к некоторой функции последовательность случайных величин
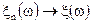
тогда
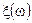
-тоже случайная величина. Действительно,
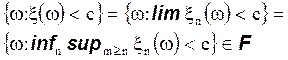
 2015-06-10
2015-06-10 949
949








