Примером последовательности случайных величин, сходящихся в среднеквадратическом к нулю является последовательность
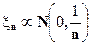
Так как
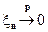 ,
,
то для любой случайной величины 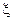
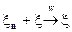 и, следовательно,
и, следовательно, 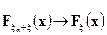 во всех точках непрерывности функции распределения
во всех точках непрерывности функции распределения 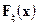 . Так как, нормальное распределение имеет плотность, то случайная величина
. Так как, нормальное распределение имеет плотность, то случайная величина 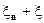 тоже имеет плотность даже для разрывной функции распределения
тоже имеет плотность даже для разрывной функции распределения 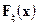 и ее функция распределения при больших n является гладким приближением функции распределения
и ее функция распределения при больших n является гладким приближением функции распределения 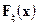 .
.
 2015-06-10
2015-06-10 441
441








