2015-06-10
384
Пусть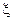 
- случайная величина с конечным математическим ожиданием, заданная на
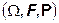
и сигма-алгебра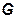 
порождена некоторым событием A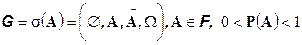 
Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом простых функций, принимающих два значения, соответственно, на множествах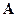 
и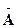 
. Обозначим их, например, 
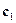и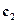 
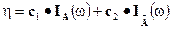
Уравнений всего 4
,
,
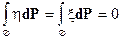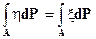
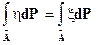
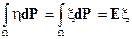причем первое из них не накладывает никаких ограничений на функцию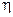 
, а четвертое следует из второго и третьего.
Так как случайная величина 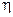постоянна на множествах и 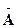то, из второго и третьего уравнений можно определить значения 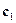и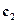
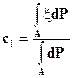
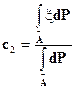
Нетрудно обобщить этот пример на случай сигма-алгебры, порожденной некоторым конечным разбиением пространства элементарных исходов.
