Пусть 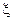 - случайно выбранная на единичном отрезке точка
- случайно выбранная на единичном отрезке точка
| Покажите, что набор всех симметричных относительно ½ борелевских подмножеств единичного отрезка является сигма-алгеброй. Множество симметрично относительно ½, если вместе с точкой х оно содержит точку 1-х. | и сигма-алгебра 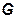 является сигма-алгеброй всех симметричных относительно точки ½ борелевских множеств единичного отрезка. Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом функций, графики которых симметричны относительно прямой х=1/2. Выбирая, в качестве множества A, симметричное при х<1/2 множество является сигма-алгеброй всех симметричных относительно точки ½ борелевских множеств единичного отрезка. Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом функций, графики которых симметричны относительно прямой х=1/2. Выбирая, в качестве множества A, симметричное при х<1/2 множество
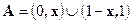 получим
получим
|
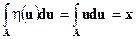
Так как график 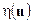 симметричен относительно центра единичного отрезка, получаем
симметричен относительно центра единичного отрезка, получаем
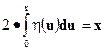
откуда следует, что
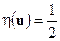
 2015-06-10
2015-06-10 404
404








