Пусть СВ  может принимать только значения
может принимать только значения 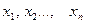 , вероятности которых соответственно равны
, вероятности которых соответственно равны 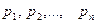 . Тогда математическое ожидание
. Тогда математическое ожидание 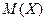 СВ определяется равенством
СВ определяется равенством
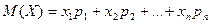 .
.
Опр. Математическим ожиданием (средним значением или первым моментом) ДСВ  называется число
называется число
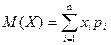 , (1)
, (1)
равное сумме произведений всех возможных значений случайной величины на их вероятности.·
Если ДСВ  принимает бесчисленное множество возможных значений, то
принимает бесчисленное множество возможных значений, то 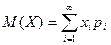 , причем математическое ожидание (МО) существует, если ряд в правой части равенства сходится абсолютно. Если же
, причем математическое ожидание (МО) существует, если ряд в правой части равенства сходится абсолютно. Если же 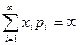 , то говорят, что МО не существует.
, то говорят, что МО не существует.
Замечание. Из определения следует, что математическое ожидание ДСВ есть величина постоянная.
МО имеет простой физический смысл: если на прямой разместить единичную массу, поместив в точки 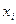 массу
массу 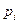 , то точка
, то точка 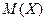 есть координата «центра тяжести» прямой.
есть координата «центра тяжести» прямой.
Например: Найти математическое ожидание СВ  , зная ее закон распределения:
, зная ее закон распределения:
 | |||
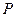 | 0,1 | 0,6 | 0,3 |
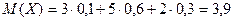 .
.
Например: Найти математическое ожидание числа появлений события  в одном испытании, если вероятность события
в одном испытании, если вероятность события  равна
равна 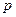 .
.
§ СВ  - число появлений события
- число появлений события  в одном испытании – может принимать только два значения:
в одном испытании – может принимать только два значения:
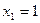 (событие наступило) с вероятностью
(событие наступило) с вероятностью 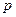 ;
;
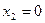 (событие не наступило) с вероятностью
(событие не наступило) с вероятностью 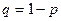 .
.
Искомое математическое ожидание 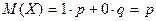 .
.
Вывод: математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Вероятностный смысл математического ожидания.
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания.
1. МО постоянной величины равно самой постоянной
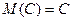 .
.
► 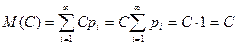 ◄
◄
2. Постоянный множитель можно выносить за знак математического ожидания
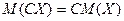 .
.
► 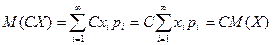 ◄
◄
3. МО произведения двух независимых случайных величин равно произведению их математических ожиданий
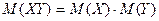 ;
;
Следствие. МО произведения нескольких взаимно независимых СВ равно произведению их математических ожиданий.
4. МО суммы двух случайных величин равно сумме математических ожиданий слагаемых:
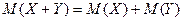
Следствие. МО суммы нескольких СВ равно сумме математических ожиданий слагаемых.
МО СВ, имеющей биномиальное распределение.
Пусть производится  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события  постоянна и равна
постоянна и равна 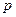 .
.
Т-ма. М атематическое ожидание 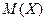 числа появлений события
числа появлений события  в
в  независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
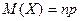 .
.
►
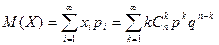 (1)
(1)
Но 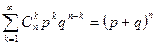 . Дифференцируем это равенство по
. Дифференцируем это равенство по 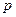 :
:
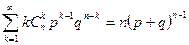 .
.
Умножим это равенство на 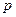 :
:
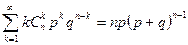 (2)
(2)
Сравнивая (1) и (2) делаем вывод:
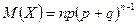 , но
, но 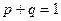 , следовательно, получаем
, следовательно, получаем 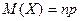 . ◄
. ◄
9.2 Дисперсия .
Дисперсиейпользуются для того, чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания.
Опр. Разность 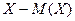 между случайной величиной и ее математическим ожиданием называют о тклонением случайной величины от ее математического ожидания. ·
между случайной величиной и ее математическим ожиданием называют о тклонением случайной величины от ее математического ожидания. ·
Свойство отклонения.
Математическое ожидание отклонения равно нулю:
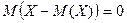 .
.
► 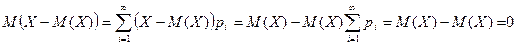 . ◄
. ◄
Опр. Дисперсией ДСВ называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
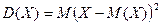 . ·
. ·
Другими словами, дисперсия есть «среднее значение квадрата отклонения СВ  от своего среднего». Посмотрим, за что эта величина отвечает.
от своего среднего». Посмотрим, за что эта величина отвечает.
Пусть СВ  принимает значения
принимает значения 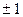 с вероятностью
с вероятностью 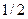 , а случайная величина
, а случайная величина 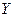 — значения
— значения 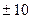 с вероятностью
с вероятностью 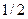 . Тогда
. Тогда 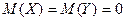 , поэтому
, поэтому 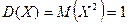 ,
, 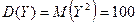 .
.
Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг ее математического ожидания.
На практике для вычисления дисперсии пользуются следующей теоремой
Т-ма. Дисперсия равна разности между математическим ожиданием квадрата случайной величины  и квадратом ее математического ожидания:
и квадратом ее математического ожидания:
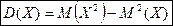 . (4)
. (4)
¨ 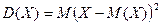 =
= 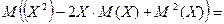
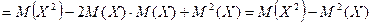 ¨
¨
Свойства дисперсии.
Все свойства дисперсии следуют из соответствующих свойств математического ожидания.
1. Дисперсия постоянной величины равна нулю:
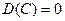 ;
;
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
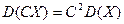 ;
;
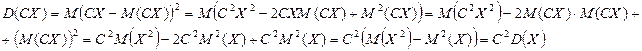
3. Дисперсия суммы и разности двух независимых случайных величин равна сумме дисперсий этих величин:
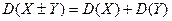 .
.
Следствие 1. Дисперсия суммы нескольких взаимно независимых СВ равна сумме дисперсий этих величин.
Например, для трех слагаемых имеем:
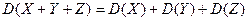 .
.
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии СВ:
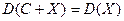 .
.
Дисперсия числа появлений события в независимых испытаниях.
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 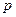 .
.
Т-ма. Дисперсия 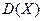 числа появлений события
числа появлений события  в
в  независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании:
независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании:
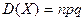 .
.
 2015-06-10
2015-06-10 5677
5677
