Предположим, что событие А может наступить только вместе с одним из попарно несовместных событий 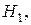
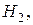 …,
…, 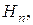 называемых гипотезами. Тогда справедлива формула полной вероятности:
называемых гипотезами. Тогда справедлива формула полной вероятности:
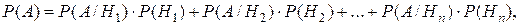
т.е. вероятность события А равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятность самих гипотез.
Безусловные вероятности 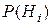 рассматриваются как априорные (доопытные) вероятности гипотез.
рассматриваются как априорные (доопытные) вероятности гипотез.
Предположим, что эксперимент произведён и в результате произошло событие А. Как изменится при этом апостериорная (послеопытная) вероятность гипотез 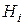 ?
?
Условные вероятности гипотез 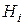 при условии, что событие А имело место, вычисляются по формулам Байеса:
при условии, что событие А имело место, вычисляются по формулам Байеса: 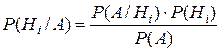 , где Р(А) вычисляется по формуле полной вероятности.
, где Р(А) вычисляется по формуле полной вероятности.
Пример 1. Имеется три партии ламп по 20, 30, 50 штук в каждой. Вероятность того, что лампы проработают заданное время, равна для каждой партии соответственно 0,7; 0,8; 0,9. Какова вероятность того, что выбранная наудачу лампа из ста данных ламп проработает заданное время?
Решение. Пусть событие А – «выбранная лампа проработает заданное время». Формулируем гипотезы: 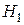 - «лампа принадлежит первой партии»,
- «лампа принадлежит первой партии», 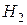 - «лампа принадлежит второй партии»,
- «лампа принадлежит второй партии», 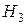 - «лампа принадлежит третьей партии».
- «лампа принадлежит третьей партии».
Тогда 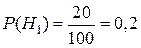 ;
; 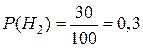 ;
; 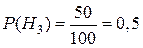 .
.
Условные вероятности по условию соответственно равны
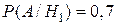 ;
; 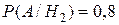 ;
; 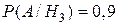 .
.
По формуле полной вероятности находим 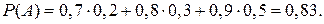
Пример 2. В первом ящике имеются 8 белых и 6 чёрных шаров, а во втором – 10 белых и 4 чёрных. Наугад выбирают ящик и шар. Известно, что вынутый шар – чёрный. Найти вероятность того, что был выбран первый ящик.
Решение. Пусть событие А – «выбран чёрный шар». Формулируем гипотезы:
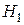 - «выбран первый ящик»,
- «выбран первый ящик», 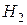 - «выбран второй ящик».
- «выбран второй ящик».
Тогда 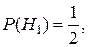
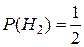 . Условные вероятности соответственно равны:
. Условные вероятности соответственно равны: 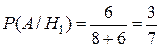 ,
, 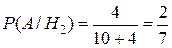 .
.
По формуле полной вероятности находим 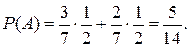
----------------------------------------------------------------------------------------------------------------
Формула полной вероятности. Формула Байеса. Стр.1
По формуле Байеса вычисляем искомую вероятность:
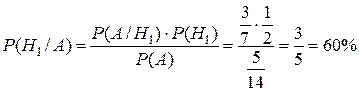 .
.
 2015-06-10
2015-06-10 8200
8200
