2015-06-10
801
Нечеткое множество является обобщением классического множества. Обобщать операции можно по-разному => определение операций будет неоднозначным, т.е. одну и ту же операцию можно определить по-разному.
Говорить об операциях над нечет. множествами возможно только, если все они проводятся на одном и том же универсальном множестве.
Т.к. неч. множество полностью определяется своей функцией принадлежности, множество и функция явл. по сути синонимами. Но одно и то же свойство может быть задано с помощью различных функций принадлежности.
Рассмотрим отношение равенства: два нечетких множества называются равными, если для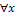 
их функции принадлежности равны: 
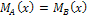, A = B.
Нечеткое множество А называется множеством нечеткого множества, если для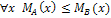 
. 
.
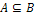Если для двух множеств неверно 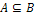ни , ни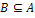 
, то говорят, что множества A и B несравнимы.
Пересечением двух нечетких множеств будем называть некоторое нечеткое множество C (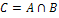
), функция принадлежности которого определяется так: 
.
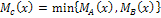Объединением двух нечетких множеств A и B, заданных на одном и том же универсальном множестве, называется множество C (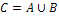
) определяется как: 
.
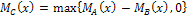Симметрической разностью нечетких множеств A и B, заданных на одном и том же универсальном множестве, называется множество C, функция принадлежности которого определяется так: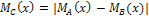 
.
Дополнением нечеткого множества A называется множество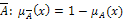 
.
В системе MatLab при моделировании именно эти определения стоят по умолчанию.
Для этих операций выполняются свойства:
1. 
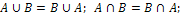
2. 
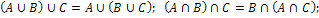
3. 
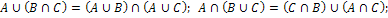
4. 
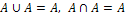- идемпотентность;
5. 
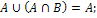
6. 
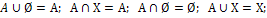
7. 
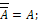
8. 
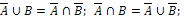
Принципиальной особенностью нечетких множеств является то, что для них не выполняются два свойства, характерные для классических множеств:
1. 
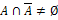
2. 
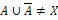
Введенные определения наиболее приближают алгебру нечетких множеств к булевым. В других определениях некоторые из 8 свойств не выполняются.
В ряде конкретных случаев целесообразно использовать не основные операции с нечеткими множествами, а альтернативные. Это может быть вызвано желанием, например, повысить адекватность модели.
