Комбинаторика

Сборник задач

По теории вероятностей

И математической статистике

Составитель С. А. Шунайлова

Челябинск

УДК

Сборник задач по теории вероятностей и математической статистике./Составитель С. А. Шунайлова, Челябинск, 2006.

Сборник задач предназначен для студентов всех специальностей 2-го курса дневного отделения Уральского филиала МАДИ.

В пособии содержатся задачи и краткие теоретические сведения по основным разделам теории вероятностей и математической статистики, изучаемым в рамках курса математики. Кроме того, пособие содержит 30 вариантов типовых расчётов по теории вероятностей и математической статистике, а также таблицы значений функций, которые используются при решении задач.

Рецензенты:

Комбинаторика

Пусть первое действие можно совершить 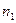различными способами, второе - 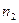различными способами,…, k-е - 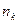различными способами. Тогда все k действий можно совершить 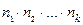различными способами. Под действием будем понимать выбор элемента из некоторого множества.

Пусть имеется множество из n различных объектов (элементов), т.е. объекты имеют или разные названия или разные номера. Пусть 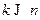. Сочетанием из n элементов по k называется любое подмножество, содержащее k элементов, взятых из данных n элементов. При этом подмножества различаются только элементами, входящими в них; порядок, в котором они расположены, не имеет значения. Число различных сочетаний из n элементов по k можно найти по формуле .

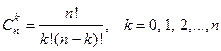Будем рассматривать множество из n (различимых) элементов. Пусть 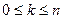– фиксированное число. Размещением из n элементов по k называется любое упорядоченное подмножество, содержащее k элементов, взятых из данных n элементов. Размещение из n элементов по k определяется элементами, входящими в это подмножество, а также порядком следования этих элементов. Число размещений из n элементов по k находится по формуле .

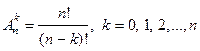В частном случае, когда k = n, размещение по n элементов из n носит название перестановки из n элементов. Все перестановки содержат одни и те же элементы; разные перестановки отличаются лишь порядком следования этих элементов. Число 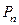различных перестановок из n элементов находится по формуле .

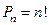Пусть имеются k групп элементов, причем в первой группе 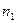неразличимых элементов, во второй группе 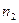неразличимых элементов, …, в k -ой группе – 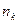неразличимых элементов. Элементы из разных групп различимы. Таким образом, имеем всего 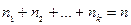элементов. Рассмотрим всевозможные упорядоченные наборы из этих элементов. Число различных таких наборов (перестановок с повторениями) равно .

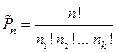1. Сколькими способами из группы в 24 человека можно выбрать двоих делегатов на конференцию?

2. Сколькими способами 5 человек могут стать в очередь друг за другом?

3. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются?

4. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе могут повторяться?

5. Сколькими способами из группы спортсменов в 18 человек можно выбрать двоих участников соревнования?

6. Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, если нечетные и четные цифры в числе чередуются и не повторяются?

7. Фотограф выстраивает в ряд трех мужчин и четырех женщин так, чтобы мужчины и женщины чередовались. Сколькими способами он может это сделать?

8. Студент сдает в сессию 3 экзамена. Сколько существует различных комбинаций оценок, которые он может получить?

9. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе идут в порядке возрастания?

10. Сколькими способами можно купить набор из трех пирожных, если в продаже имеются 4 сорта пирожных и пирожные в наборе могут повторяться?

11. Сколько шестибуквенных слов можно составить из карточек, из которых составлено слово "ананас"?

12. Сколько различных вариантов распределения оценок за контрольную работу может быть для трех студентов, если возможны оценки "2", "3", "4", "5"?

13. Сколькими способами можно выбрать тройку, семерку, туза из колоды в 52 карты?

14. Сколько шестибуквенных слов можно составить из карточек, из которых составлено слово "знания"?

15. Сколькими способами можно выбрать старосту и профорга в группе студентов из 24 человек?

16. Сколько шестибуквенных слов можно составить из карточек, из которых составлено слово "молоко"?