Функция распределения 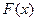 представляет собой вероятность того, что случайная величина примет значение, меньшее аргумента этой функции:
представляет собой вероятность того, что случайная величина примет значение, меньшее аргумента этой функции: 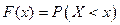 . Плотность вероятности (плотность распределения) f (x)является производной от функции распределения:
. Плотность вероятности (плотность распределения) f (x)является производной от функции распределения: 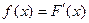 .
.
Функция плотности удовлетворяет условию нормировки: 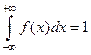 .
.
Вероятность попадания непрерывной случайной величины в интервал можно вычислить по одной из формул: 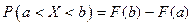 или
или 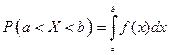 . Для непрерывной случайной величины математическое ожидание, дисперсия и среднее квадратическое отклонение определяются следующим образом:
. Для непрерывной случайной величины математическое ожидание, дисперсия и среднее квадратическое отклонение определяются следующим образом:
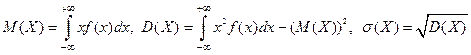 .
.
131. Плотность вероятности непрерывной случайной величины Х задана формулой. Найдите значение параметра а, функцию распределения 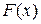 , числовые характеристики
, числовые характеристики 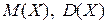 . Постройте графики функции плотности и функции распределения.
. Постройте графики функции плотности и функции распределения.
1) 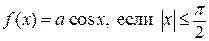 ;
;
2) 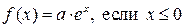 ;
;
3) 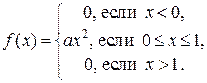
132. Плотность вероятности непрерывной случайной величины Х задается формулой 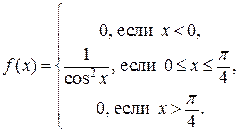 Найдите
Найдите 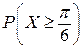 .
.
133. Случайная величина Х задана функцией распределения
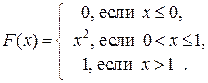
Найти плотность вероятности 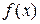 ,
, 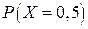 ,
, 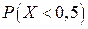 ,
, 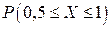 .
.
 2015-06-10
2015-06-10 621
621








