Нормальный закон распределения

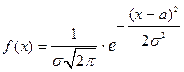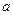Непрерывная случайная величина, имеющая нормальный закон распределения, задаётся плотность вероятности: , где и 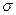— параметры. Числовые характеристики случайной величины 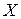, распределенной по нормальному закону, совпадают с параметрами распределения: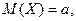 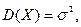а вероятность попадания 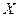в интервал 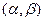подсчитывается по формул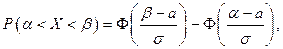е: где 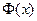– функция Лапласа, значения которой даны в таблицах в конце пособия.

140. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины Х соответственно равны 20 и 5. Написать плотность вероятности Х, функцию распределения Х и найти вероятность того, что Х примет значение, заключённое в интервале (15, 25).

141. Размеры наружных диаметров втулок распределены нормально с математическим ожиданием 1500 мм и средним квадратическим отклонением 0,4 см. Определите вероятность того, что наружный диаметр втулки: а) не меньше, чем 1,512 м; б) заключен в интервале от 1,496 до 1,504 м.

142. Браковка шариков для подшипников производится следующим образом: если шарик не проходит через отверстие диаметром 5 см, но проходит через отверстие диаметром 6 см, то его размер считается приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика Х – нормально распределенная случайная величина с математическим ожиданием, равным 5,5 см и дисперсией 1,21 см. Определите вероятность того, что шарик будет забракован.

143. Случайная величина Х (ошибка измерительного прибора) распределена по нормальному закону с дисперсией 16 мк. Систематическая ошибка прибора отсутствует. Найдите вероятность того, что в пяти независимых измерениях ошибка измерительного прибора хотя бы раз окажется в интервале 0,5 – 3,5 мк.

144. Для производства металлических трубок с внутренним диаметром, равным 0,35 см, требуется некоторая операция. Допустимые отклонения ε = 0,04 см. Предполагается, что внутренний диаметр этих трубок распределен нормально с σ = 0,025 см. Если нормальный диаметр 0,35 см в среднем выдерживается, то: а) каково математическое ожидание числа дефектных образцов в выборке объема 100; б) какова вероятность того, что в этой выборке окажется менее четырех дефектных образцов?

145. Рост взрослых мужчин в рассматриваемой совокупности является нормально распределенной случайной величиной Х. Средний рост мужчин этой совокупности 172 см. 90% мужчин имеет рост от 169 до 175 см. Найдите: а) среднее квадратическое отклонение случайной величины Х; б) долю мужчин, рост которых находится в пределах от 169 до 174 см. Какова вероятность того, что из 10 случайно отобранных мужчин у семи рост будет в пределах от 169 до 174 см?

146. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г, а его допустимый вес 2,5 г. Найдите среднее число поврежденных ружей из 1000 проверяемых.

147. Средний рост 1000 солдат равен 1,81 м со стандартным отклонением 50 мм. Полагая, что рост подчиняется нормальному закону распределения, оцените число солдат, рост которых: а) больше 1,87 м; б) лежит между 1,72 и 1,8 м. Какова вероятность того, что обмундирование третьего роста понадобится 300 солдатам. (3-й рост: 172-178 см).

148. Длина болтов, изготовляемых на автоматическом станке, является нормально распределенной случайной величиной Х. Средняя длина болтов 8,4 см, среднее квадратическое отклонение этой случайной величины 0,04 см. Найдите: а) долю болтов, длина которых от 8,32 до 8,46 см; б) долю болтов с длиной, меньшей средней; в) вероятность того, что среди 2000 болтов только у 3 болтов длина превысит 8,52 см.