| Имена испытуемых | Правильно решено | Ранг четных заданий | Ранг нечетных заданий | d | d2 | |
| Четных заданий | Нечетных заданий | |||||
| А | 10,5 | 13,5 | ||||
| Б | 8,5 | 0,5 | 0,25 | |||
| В | 6,5 | 3,5 | 12,25 | |||
| Г | ||||||
| Д | 12,5 | 15,5 | ||||
| Е | ||||||
| Ж | 15,5 | 0,5 | 0,25 | |||
| З | 8,5 | 0,5 | 0,25 | |||
| И | 6,5 | 6,5 | ||||
| К | ||||||
| Л | 6,5 | 2,5 | 6,25 | |||
| М | 12,5 | 1,5 | 2,25 | |||
| Н | ||||||
| О | ||||||
| П | 10,5 | 13,5 | ||||
| Р |
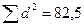
n=16; 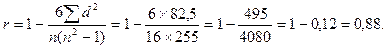
Проделана обычная ранговая корреляция. По таблице уровней значимости r0,99=0,64; полученный коэффициент превышает эту величину. Принято считать, что коэффициент надежности не должен быть ниже 0,8. Полученный коэффициент удовлетворяет этому требованию.[10]
Есть поправочная формула Спирмена – Брауна (SB) к коэффициенту надежности–гомогенности, получаемому путем расщепления. Поскольку при прочих равных условиях получаемый коэффициент будет тем выше, чем больше заданий содержится в методике, следует принять во внимание, что прием расщепления уменьшает число заданий вдвое – в этом и состоит прием. Поправочная формула такова:
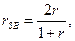
в нашем примере
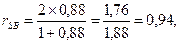
где rSB, – коэффициент с учетом поправки, а r – коэффициент, вычисленный при коррелировании двух половинок методики. Если этот последний равен 0,88, то после поправки Спирмена–Брауна коэффициент будет равен 0,94.
Поправочную формулу Спирмена–Брауна можно применять только в тех случаях, когда методика делится на половинки (расщепление). Если же в методике в процессе обработки не меняют число заданий, поправочная формула неприменима.
Величина коэффициента надежности (гомогенности) зависит от социально-психологических особенностей той выборки, по результатам испытания которой этот коэффициент устанавливался. Поэтому опубликовании методики, приводя ее основные характеристики, тор должен указать, на каком контингенте проводилась проверка надежности.
При вычислении коэффициента надежности методики, характеризующего стабильность данных, получаемых с помощью этой методики, первый коррелируемый ряд представляет собой результаты первого, а второй – повторного испытания: его рекомендуют проводить примерно через шесть недель после первого. При обоснованной необходимости этот срок может изменяться. Эти два ряда коррелируют между собой. Корреляция проводится по обычным правилам. Это прием «тест-ретест».
Для установления надежности методики существуют и некоторые другие приемы. Так, для получения коэффициента надежности практикуется прием параллельных форм.
Авторы, конструирующие методику, создают две ее формы; условно назовем их формой А и формой Б. Обе формы должны быть вполне однородны по психологической направленности, по доступности содержания заданий и по их трудности. В одном варианте формы А и Б предъявляются испытуемым одна следом за другой, причем в одной половине выборки испытуемым сначала предлагается форма А, а потом форма Б, а в другой половине выборки наоборот, сначала форма Б, а затем А. Результаты, полученные по одной и другой формам, коррелируют между собой, и полученный коэффициент трактуется как коэффициент надежности. Нетрудно заметить, что этот прием близок к приему расщепления с той разницей, что методика как бы удвоена и сравниваются не четные и нечетные задания, а две половины этой удвоенной методики. Это дает право трактовать получаемый коэффициент скорее как коэффициент надежности-гомогенности, а не надежности-стабильности. Поскольку проверке подвергается набор заданий в целом, поправочную формулу Спирмена–Брауна применить не следует.
Другой вариант использования приема параллельных форм состоит в том, что одна из форм предлагается испытуемым через какой-то интервал времени после другой, что сближает этот прием с приемом «тест-ретест». При проведении этого приема необходимо убедиться в том, что обе формы высоко коррелируют между собой согласно только что изложенному приему по надежности-гомогенности. Результаты обоих испытаний затем коррелируют между собой. Полученный коэффициент может трактоваться как коэффициент надежности-стабильности. Выше указывалось, что в приеме «тест-ретест» рекомендуется интервал между испытаниями в шесть недель. Для этого варианта приема параллельных форм данный интервал может быть уменьшен, так как испытуемый при выполнении заданий не сможет опираться на память.
Из предшествующего изложения следует, что в приемах установления надежности главную роль играет статистический метод корреляций. Несколько по-иному обстоят дела при проверке валидности методики.
Если показатели того критерия, который взят для получения коэффициента внешней валидности, имеют примерно ту же меру рассеяния, меру вариативности, что и мера рассеяния показателей самой методики, то применение корреляции правомерно.
Допустим, автор методики намерен установить ее валидность, сравнивая успешность выполнения методики с учебной деятельностью, валидность устанавливается на выборке школьников. В этом случае, как показывает практика, суммарные оценки за одну учебную четверть или за полугодие покажут примерно тот же размере колебаний, что и размах колебаний по методике-методика состоит из 20 заданий и при ее выполнении показан размах колебаний от 3 до 20. Суммарные оценки успеваемости после того, как они подсчитаны за полгода, имеют размах колебаний от 14 до 36. Такие ряды вполне возможно между собой коррелировать. Но в некоторых случаях для получения коэффициента валидности приходится сравнивать успешность выполнения диагностической методики, допустим, в тех же пределах колебаний – от 3 до 20, и производственные достижения, которые имеют всего три ступени оценок: ниже средних, средние и выше средних. Корреляцией в этом случае воспользоваться нельзя, если иметь в виду линейную корреляцию. Однако могут быть использованы некоторые другие статистические методы, показывающие существование или отсутствие связи между распределением двух рядов численностей. Простейший способ получения коэффициента валидности в описываемом случае и в других подобных случаях – метод хи-квадрат. Всех испытуемых, прошедших диагностический эксперимент, делят на три равные группы – их и сопоставляют с тремя группами, на которые были поделены испытуемые при оценке их профессиональной успеваемости.
В изучаемой выборке – 90 человек. Они делятся по профессиональным достижениям на три группы: первая – 30 испытуемых – лица с профессиональными достижениями ниже среднего уровня; вторая – 40 испытуемых–это лица со средними достижениями и третья – 20 испытуемых, их достижения выше среднего уровня. Первая группа составляет 33,3% выборки, вторая – 44,4% и третья – 22,2% выборки.
Ниже показана техника вычисления (см. табл. 20).
Таблица 20
 2015-06-14
2015-06-14 1860
1860
